Anleitung Strukturgleichungsmodellierung
- 1 Ablaufschritte einer Strukturgleichungsmodellierung
- 2 Varianzbasierte Verfahren vs. Kovarianzabasierte Verfahren
- 3 Varianzabsiertes Verfahren mit dem Pakte PLSPM
- 4 Covarianzbasiertes Verfahren mit dem Paket lavaan
- 4.1 Literatur
- 4.2 Installation von lavaan
- 4.3 SEM Analyse
- 4.3.1 Einlesen der Daten
- 4.3.2 Laden der erforderlichen Pakete
- 4.3.3 Spezifikation der Modelstruktur und Modelschätzung
- 4.3.4 Plot des Strukturmodells mit Pfadkoeffizienten
- 4.3.5 Ausgabe der Summary
- 4.3.6 Ausgabe nur Ladungen
- 4.3.7 Ausgabe nur Pfadkoeffizienten
- 4.3.8 Ausgabe Cronbachs Alpha und AVE (average variance extracted) für die Konstrukte
- 4.3.9 Ausgabe der Interkorrelationsmatrix
- 4.3.10 Vollständiger Plot mit lavaanPlot
- 4.3.11 Berechnung der Scores pro Person für die einzelnen Konstrukte
- 4.3.12 Geschlecht als moderierende Variable
- 4.3.13 MGA mit lavaan
- 4.3.14 Tipps zur Dokumentation
- 4.3.15 Schätzverfahren
- 4.3.16 Güte des Gesamtmodells
- 5 Prüfkriterien SEM-Analyse
- 6 Literatur
1 Ablaufschritte einer Strukturgleichungsmodellierung
1.1 Hypothesenbildung
Im ersten Schritt erfolgt die theoretisch fundierte Festlegung der zu berücksichtigenden Variablen und der Beziehungen zwischen diesen Variablen. Hierbei lassen sich drei verschiedene Ausgangssituationen differenzieren, die sich hinsichtlich ihres konfirmatorischen bzw. explorativen Charakters unterscheiden (vgl. Jöreskog/Sörbom 1993, S. 115):
- streng konfirmatorischer Hypothesentest,
- Vergleich mehrerer plausibler Modelle, oder
- ausgehend von einem vorläufigen Modell, die theoriegeleitete, schrittweise Modellmodifikation bis die Anpassungsgüte zufriedenstellend ausfällt. (Diese Vorgehensweise ist in der Forschungspraxis besonders häufig anzutreffen.)
1.2 Erstellung eines Pfaddiagramms
Anschließend erfolgt die grafische Darstellung der Beziehungszusammenhänge.
1.3 Spezifikation der Modellstruktur
Im dritten Ablaufschritt erfolgt mit Hilfe von Matrizengleichungen die Überführung des Pfaddiagramms bzw. der Hypothesen in mathematische Gleichungen.
1.4 Identifikation der Modellstruktur
Als viertes wird das Gleichungssystem auf seine Lösbarkeit hin, d.h. auf eindeutige Bestimmbarkeit aller zu schätzenden Parameter, überprüft.
1.5 Modellschätzung
Das für die vorliegende Untersuchung stellt für die Modellschätzung eine Reihe von Methoden zur Verfügung, deren Anwendung auf spezifischen Voraussetzungen beruht. Die Schätzung der Parameter des Modells kann auf unterschiedliche Weise erfolgen. Grundsätzlich gibt es zwei verschiedene Ansätze.
Für die meisten Forscher ist die SEM gleichbedeutend mit der Durchführung der kovarianzbasierten SEM (CB-SEM). Das Ziel der CB-SEM ist das Testen von Theorien, die Bestätigung von Theorien oder der Vergleich von alternativen Theorien. Die Parameterschätzung des Modells erfolgt gleichzeitig. SEM - Partielle Kleinstquadrate SEM (PLS-SEM).
Das Ziel bei der varianzbasierten SEM (Partial Least Squares SEM oder PLS-SEM) ist die Vorhersage wichtiger Zielkonstrukte oder die Identifikation wichtiger Treiberkonstrukte. Die Faktorwerte werden zunächst sukzessive für die Messmodelle ermittelt und dann in einem zweiten Schritt als Messwerte für die latenten Variablen in einer Regressionsanalyse verwendet.
1.6 Beurteilung der Ergebnisse der Modellschätzung
Im letzten Schritt werden die Teilstrukturen sowie die Modellstruktur als Ganzes mit Hilfe verschiedener Gütekriterien überprüft.
2 Varianzbasierte Verfahren vs. Kovarianzabasierte Verfahren
Grundsätzlich gibt es zwei Möglichkeiten Strukturgleichungsmodelle zu rechnen. Ich stelle hier die Auswertung mit beiden Verfahren vor und verwende jeweils Pakete in R.
Für Varianzabsierte Verfahren:
PLSPMFür Covarianzbasierte Verfahren:
lavaan
Weitere Erläuterungen und Unterscheidung der beide Verfahren unter Forschungsmethoden/Strukturgleichungsmodellierung
Wichtiger Hinweis: Ich zeige hier nur, wie die Auswertung funktioniert. Um die Ergebnisse zu interpretieren, verwenden Sie bitte die jeweilige Literatur für PLS-PM oder lavaan
3 Varianzabsiertes Verfahren mit dem Pakte PLSPM
3.1 Literatur
Die nachfolgende Vorgehensweise ist in Anlehnung an
Introduction to the R package plspm
Die nachfolgende Dokumentation ersetzt in keinem Fall das Lesen der Literatur!!!!
3.2 Installation von PLSPM
Zuerst das Paket devtools installiert und dann das Pakt plspm über nachfolgende Befehle.
- Installation von “devtools”
install.packages("devtools")
library(devtools)
- Installation von “plspm”
install_github("gastonstat/plspm")
3.3 Datenimport
Siehe Rubrik Daten via API Schnittstelle
Die Daten können auch einfach als csv in R eingelesen werden mittels data<-read.csv2()
3.4 Laden der erforderlichen Pakete in R
library(mosaic)
library(plspm)
3.5 Daten für die Analyse vorbereiten
Eventuell bzw. ziemlich sicher müssen die Daten vorher vorbereitet werden.
Vorbereitung heißt:
- Daten richtig codieren (negativ formulierte Items müssten recodiert werden)
- Missing values ersetzen (Hier kann es unter Umständen Probleme mit PLSPM geben, sollten Missing values vorhanden sein)
3.6 PLS Analyse
3.7 Pfadmodell erstellen
Jetzt kommt das Wichtigste, das Pfadmodell definieren.
Im nachfolgenden Beispiel ist das Modell sehr einfach. Die Matrix spiegelt hierbei das Pfadmodell wider.
Aus der Theorie haben wir folgendes Modell abgeleitet, welches wir anhand unserer Daten überprüfen wollen. Siehe zur Konzeption den Leitfaden
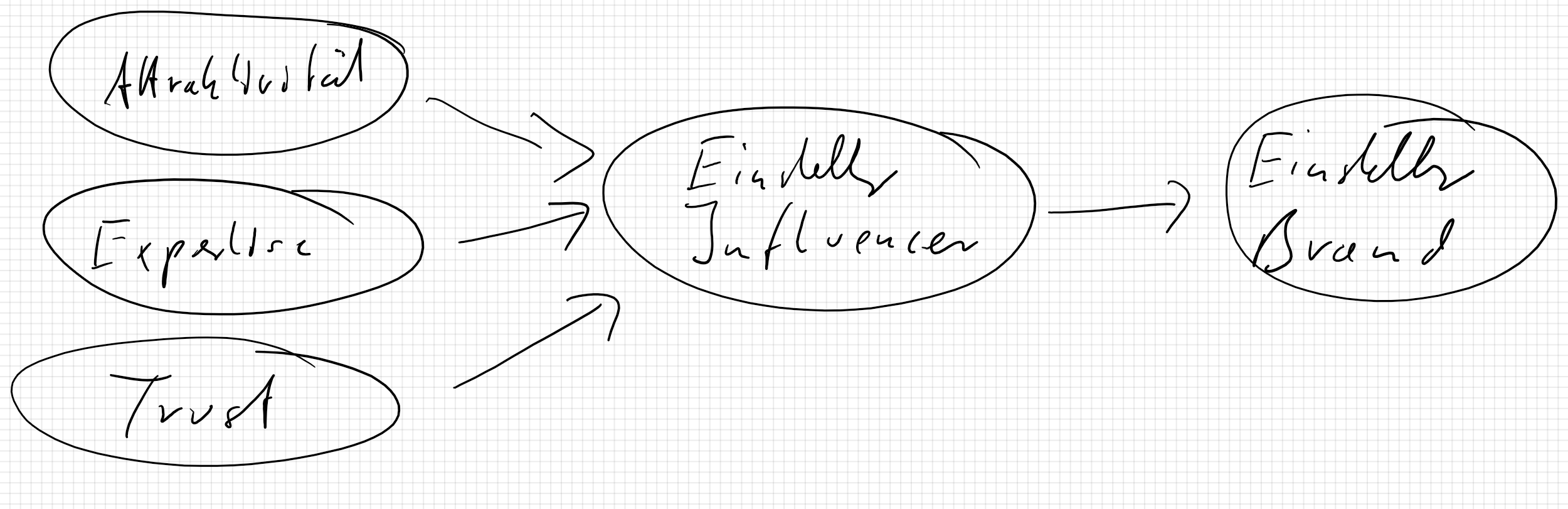 Exogene Variablen sind Attraktivität, Expertise, Trust. Endogene Variablen sind Einstellung zu Influencer und Einstellung zu Brand.
Exogene Variablen sind Attraktivität, Expertise, Trust. Endogene Variablen sind Einstellung zu Influencer und Einstellung zu Brand.
3.8 Schritte der PLS Analyse
3.8.1 Einlesen der Daten
Siehe hierzu auch mit den gleichen Daten im Repetitorium
data<-read.csv2("http://www.gansser.de/data/Daten_IM.csv")Die Daten sind bereits bereinigt, ohne NAs und vollständig.
3.8.2 Erstellen der Pfade
Im nachfolgenden Beispiel ist das Modell sehr einfach. Die Matrix spiegelt hierbei das Pfadmodell wieder. Aus der Theorie wissen wir, dass die Attraktivität des Influencers (in der Matrix in der ersten Zeile r1) einen Einfluss auf die Einstellung zum Influencer hat. Deshalb schreiben wir in Zeile vier und Spalte eins einen 1. Eine 0 bedeutet kein Einfluss. Es wird immer von oben (Spalte) nach unten (Zeile) gelesen. Die Matrix ist symmetrisch und es sollte nur die untere Triangel ausgefüllt werden bzw. mit Einsen besetzte sein. Die Matrix heißt deshalb auch untere Triangelmatrix.
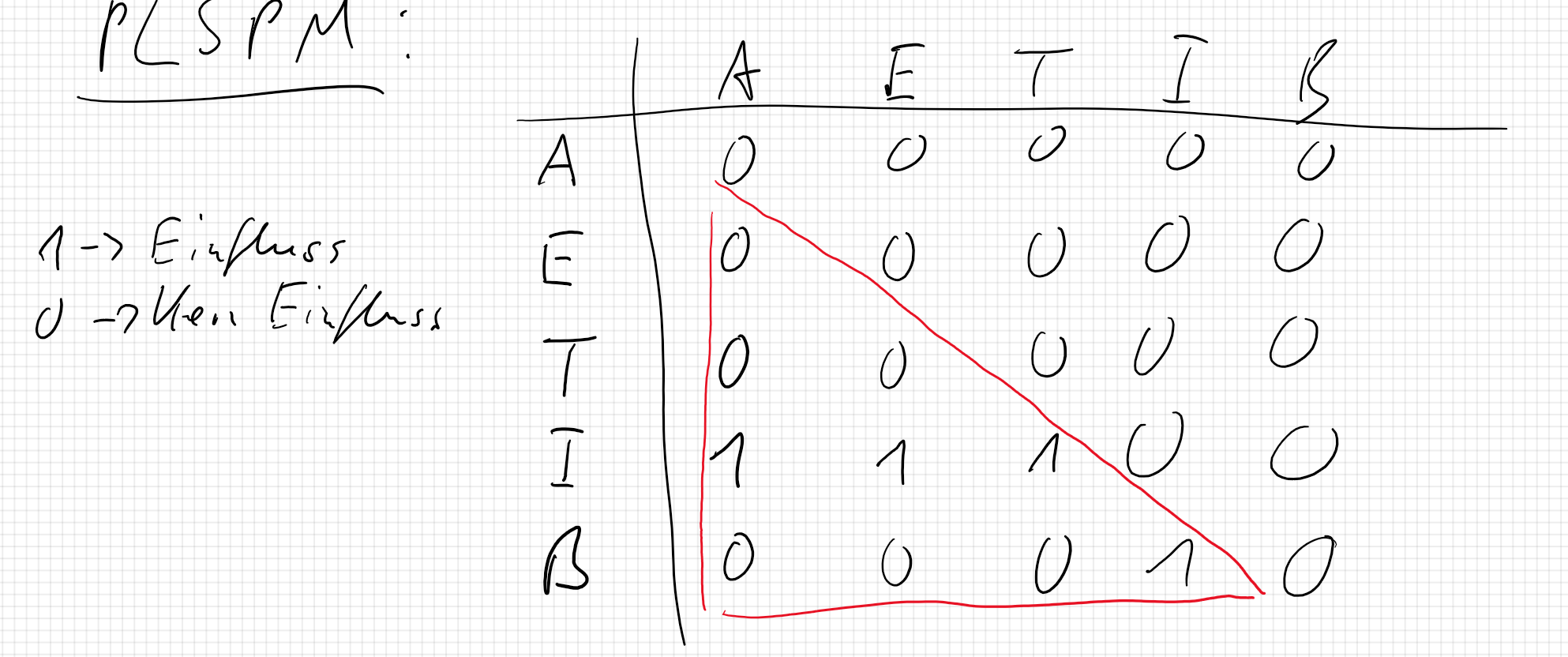
library(plspm)## Warning: Paket 'plspm' wurde unter R Version 4.4.1 erstelltr1 = c(0, 0, 0, 0, 0)
r2 = c(0, 0, 0, 0, 0)
r3 = c(0, 0, 0, 0, 0)
r4 = c(1, 1, 1, 0, 0)
r5 = c(0, 0, 0, 1, 0)
path = rbind(r1, r2, r3, r4, r5)
rownames(path) = c("Attractivity", "Expertise", "Trust", "Influencer", "Brand")
colnames(path) = rownames(path)
innerplot(path)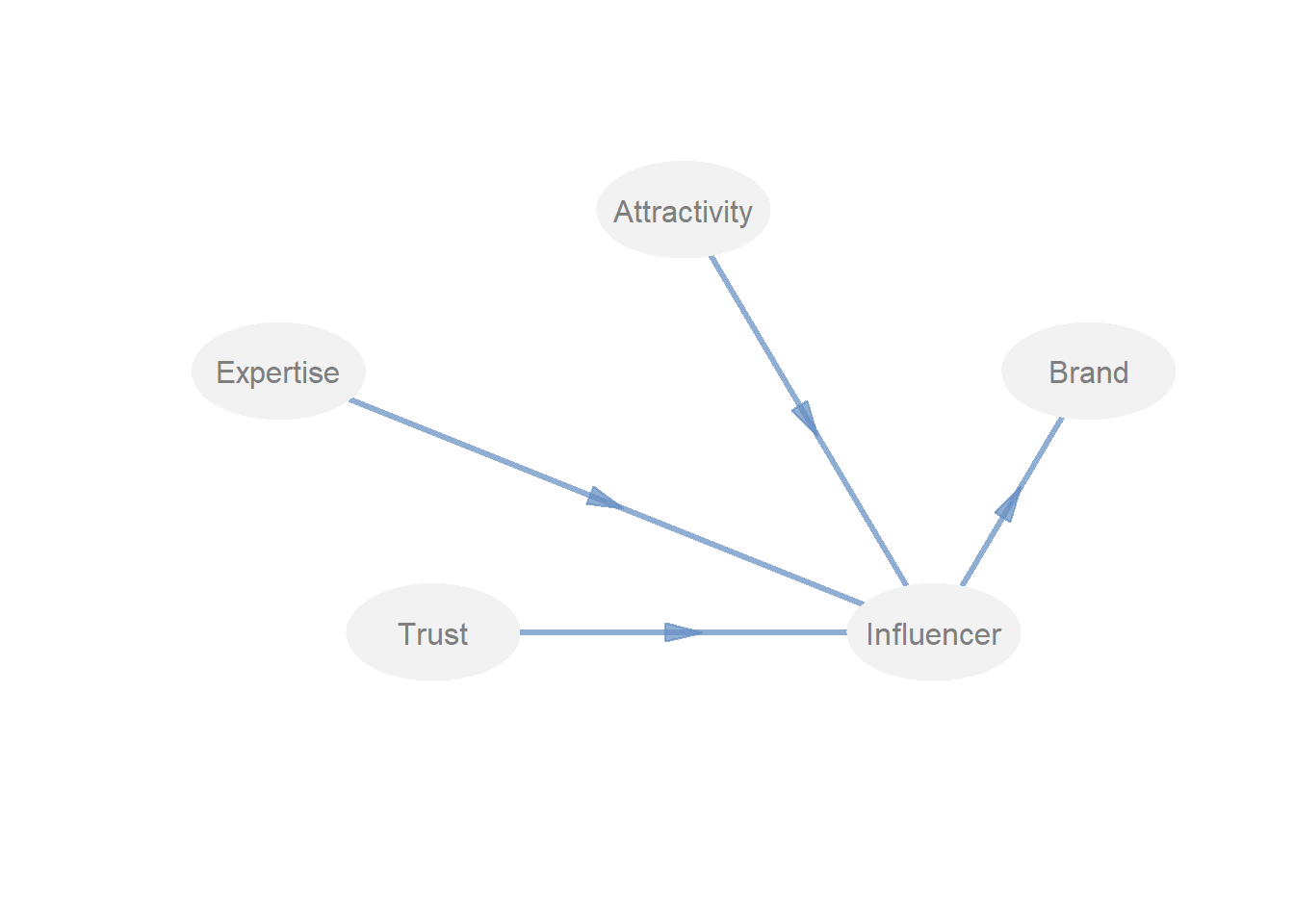
Mit innerplot(path) kann dann das Pfadmodell ausgegeben werden und geprüft werden, ob alle Pfade richtig gesetzt sind.
3.8.3 Zuweisung der Items zu Modell
Das Konstrukt GFK wurde in der Umfrage operationalisiert mit den Items von Variable 20 bis 43, usw.
Deswegen bilden wir die Blöcke für alle Konstrukte:
t(colnames(data))## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
## [1,] "Geschlecht" "Alter" "A1" "A2" "A3" "A4" "A5" "E1" "E2" "E3" "E4" "E5"
## [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22] [,23] [,24]
## [1,] "T1" "T2" "T3" "T4" "T5" "T6" "I1" "I2" "I3" "I4" "B1" "B2"
## [,25] [,26] [,27]
## [1,] "B3" "B4" "B5"blocks = list(3:7, 8:12, 13:18, 19:22, 23:27)3.8.4 Festlegung der Art Messmodelle
Es gibt zwei Möglichkeiten: formativ und reflektiv
Siehe hierzu Kapitel Strukturgleichungsmodelle in den Forschungsmethoden
Wichtiger Hinweis: Wenn ein Modell mit formativen Konstrukten gemessen wird, dann bleibt nur die Analyse mit PLSPM.
Reflektive Konstrukte sind Konstrukte mit dem Mode A
Formative Konstrukte sind Konstrukte mit dem Mode B
In unserem Beispiel haben wir 4 reflektive Blöcke, deswegen wiederholen wir 4 Mal A.
modes = rep("A", 5)Sollen wir einen oder mehrere Blöcke haben die A oder B sind, könnte man schreiben modes = c("A", "B", etc.)
3.8.5 Durchführung der PLSPM Analyse mit Bootstrap Validierung.
pls = plspm(data, path, blocks, modes = modes)
summary(pls)## PARTIAL LEAST SQUARES PATH MODELING (PLS-PM)
##
## ----------------------------------------------------------
## MODEL SPECIFICATION
## 1 Number of Cases 250
## 2 Latent Variables 5
## 3 Manifest Variables 25
## 4 Scale of Data Standardized Data
## 5 Non-Metric PLS FALSE
## 6 Weighting Scheme centroid
## 7 Tolerance Crit 1e-06
## 8 Max Num Iters 100
## 9 Convergence Iters 3
## 10 Bootstrapping FALSE
## 11 Bootstrap samples NULL
##
## ----------------------------------------------------------
## BLOCKS DEFINITION
## Block Type Size Mode
## 1 Attractivity Exogenous 5 A
## 2 Expertise Exogenous 5 A
## 3 Trust Exogenous 6 A
## 4 Influencer Endogenous 4 A
## 5 Brand Endogenous 5 A
##
## ----------------------------------------------------------
## BLOCKS UNIDIMENSIONALITY
## Mode MVs C.alpha DG.rho eig.1st eig.2nd
## Attractivity A 5 0.915 0.937 3.74 0.545
## Expertise A 5 0.964 0.972 4.37 0.212
## Trust A 6 0.973 0.978 5.28 0.226
## Influencer A 4 0.938 0.955 3.37 0.325
## Brand A 5 0.971 0.977 4.47 0.177
##
## ----------------------------------------------------------
## OUTER MODEL
## weight loading communality redundancy
## Attractivity
## 1 A1 0.242 0.882 0.778 0.000
## 1 A2 0.233 0.879 0.773 0.000
## 1 A3 0.251 0.884 0.781 0.000
## 1 A4 0.218 0.807 0.651 0.000
## 1 A5 0.211 0.870 0.757 0.000
## Expertise
## 2 E1 0.190 0.919 0.844 0.000
## 2 E2 0.213 0.948 0.899 0.000
## 2 E3 0.221 0.944 0.891 0.000
## 2 E4 0.229 0.938 0.880 0.000
## 2 E5 0.215 0.926 0.858 0.000
## Trust
## 3 T1 0.184 0.927 0.860 0.000
## 3 T2 0.169 0.931 0.867 0.000
## 3 T3 0.186 0.946 0.895 0.000
## 3 T4 0.177 0.949 0.901 0.000
## 3 T5 0.167 0.919 0.845 0.000
## 3 T6 0.182 0.956 0.914 0.000
## Influencer
## 4 I1 0.277 0.924 0.854 0.588
## 4 I2 0.281 0.943 0.890 0.612
## 4 I3 0.286 0.938 0.880 0.605
## 4 I4 0.244 0.864 0.747 0.514
## Brand
## 5 B1 0.209 0.935 0.875 0.264
## 5 B2 0.208 0.948 0.899 0.271
## 5 B3 0.215 0.954 0.911 0.275
## 5 B4 0.209 0.937 0.878 0.265
## 5 B5 0.217 0.955 0.912 0.275
##
## ----------------------------------------------------------
## CROSSLOADINGS
## Attractivity Expertise Trust Influencer Brand
## Attractivity
## 1 A1 0.882 0.419 0.461 0.638 0.331
## 1 A2 0.879 0.517 0.510 0.614 0.357
## 1 A3 0.884 0.441 0.457 0.662 0.308
## 1 A4 0.807 0.452 0.475 0.575 0.342
## 1 A5 0.870 0.427 0.420 0.556 0.308
## Expertise
## 2 E1 0.444 0.919 0.644 0.518 0.373
## 2 E2 0.492 0.948 0.653 0.581 0.405
## 2 E3 0.506 0.944 0.697 0.602 0.392
## 2 E4 0.479 0.938 0.692 0.625 0.468
## 2 E5 0.513 0.926 0.685 0.588 0.425
## Trust
## 3 T1 0.527 0.680 0.927 0.721 0.524
## 3 T2 0.486 0.651 0.931 0.665 0.504
## 3 T3 0.517 0.699 0.946 0.730 0.547
## 3 T4 0.513 0.657 0.949 0.696 0.535
## 3 T5 0.480 0.698 0.919 0.655 0.500
## 3 T6 0.500 0.679 0.956 0.714 0.520
## Influencer
## 4 I1 0.627 0.581 0.718 0.924 0.525
## 4 I2 0.656 0.590 0.708 0.943 0.527
## 4 I3 0.687 0.619 0.724 0.938 0.500
## 4 I4 0.623 0.500 0.570 0.864 0.463
## Brand
## 5 B1 0.346 0.396 0.508 0.513 0.935
## 5 B2 0.362 0.411 0.508 0.510 0.948
## 5 B3 0.377 0.424 0.515 0.528 0.954
## 5 B4 0.330 0.431 0.554 0.513 0.937
## 5 B5 0.383 0.431 0.546 0.534 0.955
##
## ----------------------------------------------------------
## INNER MODEL
## $Influencer
## Estimate Std. Error t value Pr(>|t|)
## Intercept 1.92e-16 0.0356 5.39e-15 1.00e+00
## Attractivity 4.18e-01 0.0434 9.64e+00 7.32e-19
## Expertise 6.83e-02 0.0529 1.29e+00 1.97e-01
## Trust 4.70e-01 0.0535 8.78e+00 2.88e-16
##
## $Brand
## Estimate Std. Error t value Pr(>|t|)
## Intercept -1.52e-16 0.0531 -2.86e-15 1.00e+00
## Influencer 5.49e-01 0.0531 1.04e+01 4.06e-21
##
## ----------------------------------------------------------
## CORRELATIONS BETWEEN LVs
## Attractivity Expertise Trust Influencer Brand
## Attractivity 1.000 0.521 0.537 0.707 0.380
## Expertise 0.521 1.000 0.722 0.625 0.443
## Trust 0.537 0.722 1.000 0.744 0.556
## Influencer 0.707 0.625 0.744 1.000 0.549
## Brand 0.380 0.443 0.556 0.549 1.000
##
## ----------------------------------------------------------
## SUMMARY INNER MODEL
## Type R2 Block_Communality Mean_Redundancy AVE
## Attractivity Exogenous 0.000 0.748 0.00 0.748
## Expertise Exogenous 0.000 0.874 0.00 0.874
## Trust Exogenous 0.000 0.880 0.00 0.880
## Influencer Endogenous 0.688 0.843 0.58 0.843
## Brand Endogenous 0.302 0.895 0.27 0.895
##
## ----------------------------------------------------------
## GOODNESS-OF-FIT
## [1] 0.6483
##
## ----------------------------------------------------------
## TOTAL EFFECTS
## relationships direct indirect total
## 1 Attractivity -> Expertise 0.0000 0.0000 0.0000
## 2 Attractivity -> Trust 0.0000 0.0000 0.0000
## 3 Attractivity -> Influencer 0.4184 0.0000 0.4184
## 4 Attractivity -> Brand 0.0000 0.2299 0.2299
## 5 Expertise -> Trust 0.0000 0.0000 0.0000
## 6 Expertise -> Influencer 0.0683 0.0000 0.0683
## 7 Expertise -> Brand 0.0000 0.0375 0.0375
## 8 Trust -> Influencer 0.4696 0.0000 0.4696
## 9 Trust -> Brand 0.0000 0.2580 0.2580
## 10 Influencer -> Brand 0.5494 0.0000 0.54943.8.6 Durchführung der PLS Analyse mit verschiedenen Gruppen
Die Modellprüfung wird stets mit dem globalen Modell (ohne Gruppen) durchgeführt. Es können aber auch Teilmodelle analysiert werden. Hier steht nicht die Modellprüfung im Vordergrund, sondern die Pfadkoeffizienten der Teilmodelle und insbesondere die Differenz der Pfadmodell. Die Differenz wir dann mittels t-test auf Signifikanz geprüft.
Hierzu muss als erstes ein Teildatensatz extrahiert werden. Wir nehmen hier zunächst zwei Merkmalsausprägungen aus einer Gruppenvariable. Wichtig hierbei ist, dass die Gruppenvariable nicht mehr als zwei Merkmalsausprägungen hat. Sollten mehr als zwei vorhanden sein, muss ein Teildatensatz gebildet werden und die gespeicherte Information über die levels (mehr als zwei) gelöscht werden. Die Gruppenvariable sollte auch immer als Faktor definiert sein.
Beispiel:
data$Geschlecht<-as.factor(data$Geschlecht)
library(dplyr)
mga<-data%>%
select(Geschlecht)%>%
droplevels()
#Anschließend kann über das Bootstrapping ein Gruppenvergleich der Pfadkoeffizienten vorgenommen werden:
mga_boot = plspm.groups(pls, mga$Geschlecht, method = "bootstrap")
#Anschließend können die Unterschiede zwischen den Pfadkoeffizienten der beiden Teilmodelle analysiert und interpretiert werden:
mga_boot$test## global group.maennlich group.weiblich diff.abs t.stat
## Attractivity->Influencer 0.4184 0.4132 0.3800 0.0332 0.3627
## Expertise->Influencer 0.0683 0.1186 -0.0007 0.1193 0.8770
## Trust->Influencer 0.4696 0.4404 0.5422 0.1018 0.7940
## Influencer->Brand 0.5494 0.5968 0.5187 0.0781 0.6232
## deg.fr p.value sig.05
## Attractivity->Influencer 248 0.3586 no
## Expertise->Influencer 248 0.1907 no
## Trust->Influencer 248 0.2140 no
## Influencer->Brand 248 0.2669 noTipp: Um die Ergebnisse einer Datenanalyse mit PLSPM zu dokumentieren empfehle ich sich an die Literatur von PLS Path Modeling with R zu halten. In Kapitel vier wird Schritt für Schritt erklärt, wie die Ergebnisse zu dokumentieren und zu interpretieren sind.
4 Covarianzbasiertes Verfahren mit dem Paket lavaan
4.1 Literatur
4.2 Installation von lavaan
install.packages(“lavaan”)
4.3 SEM Analyse
Achtung, die Logik für die Anwendung der CB-SEM ist eine andere wie für PLS.
Es macht z. B. keinen Sinn hier vorher eine Dimensionsreduktion durchzuführen, da das vorgehen ja nicht explorativ ist, sondern konfirmatorisch.
4.3.1 Einlesen der Daten
Achtung: Vor dem Einlesen der Daten sollte gewährleistet werden, ob die Anzahl der Auskunftspersonen für die Analyse ausreicht. Hierzu gibt es einen Daumenregel: Anzahl Parameter im Modell x 5.
Wie bestimmt man die Anzahl Parameter? Entweder man liest das Modell ein und macht eine Auswertung. In der Summary (s. u. ) steht im ersten Teil die Anzahl Parameter. Oder man rechnet dies von Hand aus. Grob wäre das: Anzahl Items x 2 + Anzahl Hypothesen x 2.
Bei dem nachfolgend analysierten Modell handelt es sich um das identische Modell aus dem Kapitel PLS-PM und den identischen Daten.
data<-read.csv2("http://www.gansser.de/data/Daten_IM.csv")Die Daten sind bereits bereinigt, ohne NAs und vollständig.
4.3.2 Laden der erforderlichen Pakete
library(lavaan)
library(semTools)
library(semPlot)
library(imputeTS)
library(lavaanPlot) # ggf. Installation über devtools::install_github("alishinski/lavaanPlot")
library(psych)4.3.3 Spezifikation der Modelstruktur und Modelschätzung
Das Modell wird zunächst zweigeteilt definiert, zuerst die Indikatoren, die die Konstrukte messen und dann die Regressionsbeziehung. Dies ist für Studierenden die einfachere Variante, da zuerst die latenten Variablen definiert werden und im nächsten Schritt die Pfadbeziehung. Die Ausgabe ist hierbei auch einfach zu lesen, da die Pfadbeziehungen unter dem Abschnitt Regression ausgegeben wird.
semModel_IM <- "
# Measurement Model
Brand =~ B1 + B2 + B3 + B4 + B5
Influencer =~ I1 + I2 + I3 + I4
Attractivity =~ A1 + A2 + A3 + A4 + A5
Expertise =~ E1 + E2 + E3 + E4 + E5
Vertrauen =~ T1 + T2 + T3 + T4 + T5 + T6
# regressions
Influencer ~ Attractivity + Expertise + Vertrauen
Brand ~ Influencer"
fit <- sem(semModel_IM, data=data, estimator = "ml", std.lv=TRUE) Tipp:
Wenn Sie alle Kovarianzen der latenten Variablen in einem CFA-Modell auf orthogonale Bedingungen beschränken müssen, gibt es eine Abkürzung. Sie können die Kovarianzformeln in der Modellsyntax weglassen und orthogonal = TRUE als Argument hinzufügen
Ebenso lassen sich 0/1 codierte endogene Konstrukte in das Modell einfügen. Das ist nicht optimal, weil solche Konstrukte einfach weniger Streuung haben als Konstrukte die bspw. auf einer Skla von 1-7 erhoben wurden, aber sei es wie es sei. Sie können dann als Argument ordered ="Konstrukt" hinzufügen. Wenn Sie mehrere Konstrukte 0/1 codiert haben geht das mit ordered = "c("Konstrukt1","Kontrukt2“, usw).
Kompakte Schreibweise:
semModel_IM <- "
# Messmodell
Brand =~ B1 + B2 + B3 + B4 +B5
Influencer =~ Brand + I1 + I2 + I3 + I4
Attractivity =~ Influencer + A1 + A2 + A3 + A4 +A5
Expertise =~ Influencer + E1 + E2 + E3 + E4 + E5
Vertrauen =~ Influencer + T1 + T2 + T3 + T4 + T5 + T6"Die Modelldefintion im kompakten Modell ist folgendermaßen zu lesen:
- Brand besteht aus den Variablen B1 + B2 + B3 + B4 +B5
- Influencer beeinflusst Brand und besteht aus den Variablen I1 + I2 + I3 + I4
- usw.
Wichtig ist beim Kompakten Modell, dass in einem graphischen Modell mit den endogenen Konstrukten begonnen wird.
Will man Konstrukte höherer Ordnung definieren, müssen die einzelnen Konstrukte durch die Items erst definiert werden, um dann wiederum das Konstrukt höherer Ordnung zu messen.
Beispiel (Items sind im Datensatz nicht enthalten):
intention wird gemessen durch die Konstrukte consumption, energy, food und mobilty und hat selbst keine Items.
consumption =~ Y6.1 + Y6.2 + Y6.3 + Y6.4
energy =~ Y6.7 + Y6.8 + Y6.9 + Y6.10
food =~ Y6.11 + Y6.12 + Y6.13
mobility =~ Y6.14 + Y6.15 + Y6.16
intention =~ consumption + energy + food + mobility
4.3.4 Plot des Strukturmodells mit Pfadkoeffizienten
semPaths(fit, what="std", fade=F, residuals=F,
layout="tree2", structural=T, exoCov=F, nCharNodes=10, edge.label.cex=.8,
rotation = 2, sizeLat=10, nDigits = 3)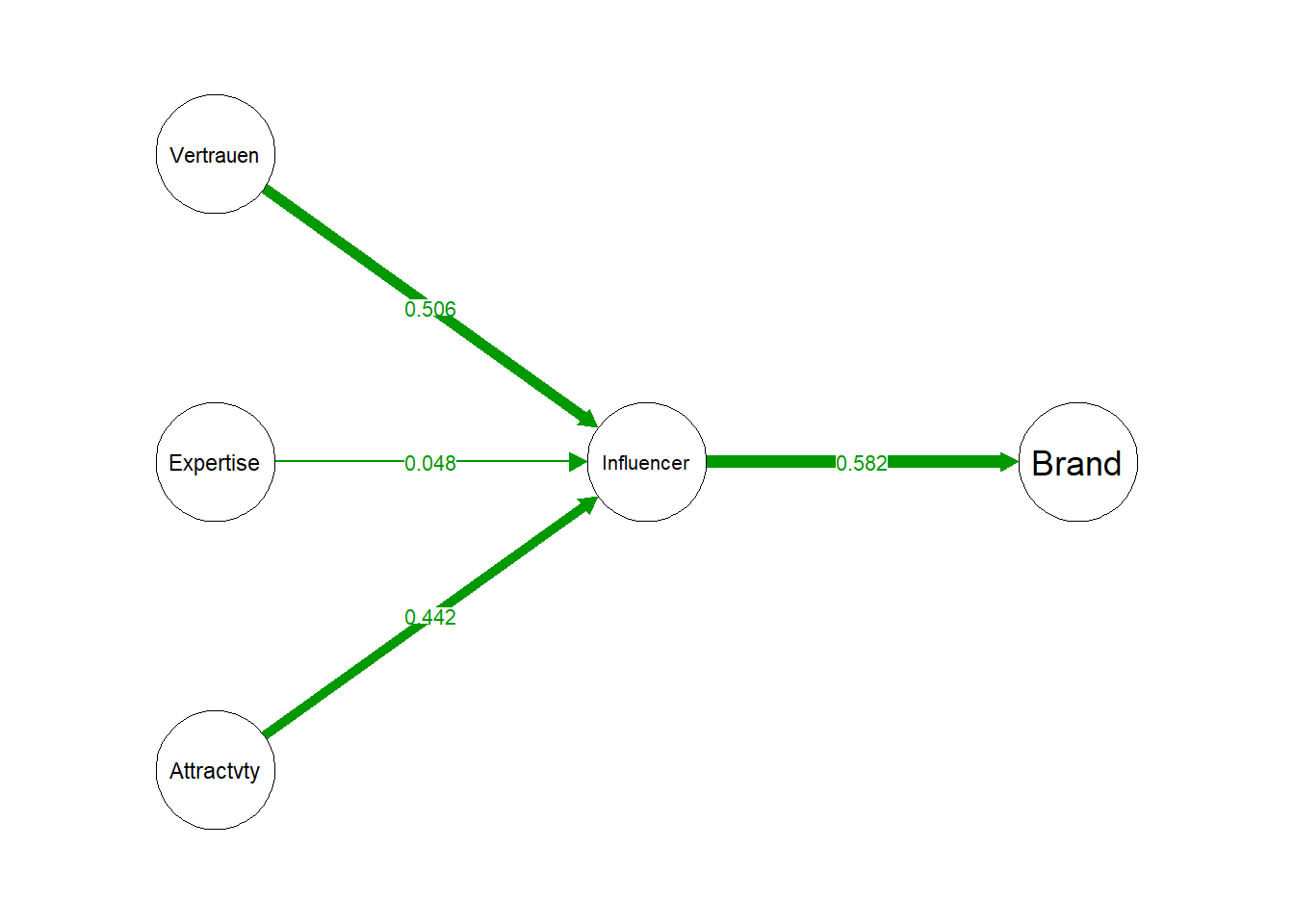
4.3.5 Ausgabe der Summary
Tipp: Wenn die Summary einmal ausgegeben wurde, auch wenn die Befragung noch nicht beendet ist, können Sie die Anzahl geschätzter Parameter, die in der Summary ausgegeben wird, mit 5 multiplizieren. Mit diesem Ergebnis kennen Sie nun die Zielgröße für die Anzahl APN die Sie befragen sollten, um anständige Ergebnisse aus der Analyse zu bekommen.
summary(fit, fit.measures=T, rsquare=T, standardized = T)## lavaan 0.6.17 ended normally after 55 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 57
##
## Number of observations 250
##
## Model Test User Model:
##
## Test statistic 466.706
## Degrees of freedom 268
## P-value (Chi-square) 0.000
##
## Model Test Baseline Model:
##
## Test statistic 8102.199
## Degrees of freedom 300
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.975
## Tucker-Lewis Index (TLI) 0.971
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -8285.469
## Loglikelihood unrestricted model (H1) -8052.116
##
## Akaike (AIC) 16684.938
## Bayesian (BIC) 16885.661
## Sample-size adjusted Bayesian (SABIC) 16704.967
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.054
## 90 Percent confidence interval - lower 0.046
## 90 Percent confidence interval - upper 0.063
## P-value H_0: RMSEA <= 0.050 0.183
## P-value H_0: RMSEA >= 0.080 0.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.049
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Brand =~
## B1 1.271 0.070 18.212 0.000 1.563 0.911
## B2 1.188 0.062 19.066 0.000 1.460 0.936
## B3 1.189 0.061 19.470 0.000 1.461 0.948
## B4 1.212 0.066 18.331 0.000 1.490 0.914
## B5 1.172 0.060 19.505 0.000 1.440 0.949
## Influencer =~
## I1 0.729 0.048 15.268 0.000 1.493 0.902
## I2 0.678 0.043 15.688 0.000 1.389 0.924
## I3 0.679 0.043 15.736 0.000 1.391 0.927
## I4 0.597 0.045 13.288 0.000 1.223 0.801
## Attractivity =~
## A1 1.343 0.079 16.961 0.000 1.343 0.867
## A2 1.524 0.096 15.831 0.000 1.524 0.831
## A3 1.215 0.072 16.842 0.000 1.215 0.864
## A4 1.271 0.096 13.275 0.000 1.271 0.737
## A5 1.423 0.089 16.009 0.000 1.423 0.837
## Expertise =~
## E1 1.717 0.094 18.214 0.000 1.717 0.897
## E2 1.773 0.090 19.694 0.000 1.773 0.938
## E3 1.812 0.093 19.560 0.000 1.812 0.934
## E4 1.671 0.088 18.938 0.000 1.671 0.917
## E5 1.610 0.087 18.483 0.000 1.610 0.905
## Vertrauen =~
## T1 1.460 0.078 18.698 0.000 1.460 0.910
## T2 1.599 0.085 18.895 0.000 1.599 0.915
## T3 1.564 0.080 19.635 0.000 1.564 0.935
## T4 1.621 0.082 19.814 0.000 1.621 0.940
## T5 1.678 0.091 18.441 0.000 1.678 0.902
## T6 1.697 0.084 20.269 0.000 1.697 0.952
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Influencer ~
## Attractivity 0.905 0.120 7.509 0.000 0.442 0.442
## Expertise 0.098 0.117 0.840 0.401 0.048 0.048
## Vertrauen 1.037 0.141 7.347 0.000 0.506 0.506
## Brand ~
## Influencer 0.349 0.042 8.288 0.000 0.582 0.582
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Attractivity ~~
## Expertise 0.545 0.048 11.277 0.000 0.545 0.545
## Vertrauen 0.557 0.047 11.810 0.000 0.557 0.557
## Expertise ~~
## Vertrauen 0.738 0.031 23.981 0.000 0.738 0.738
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .B1 0.502 0.052 9.611 0.000 0.502 0.170
## .B2 0.300 0.034 8.872 0.000 0.300 0.123
## .B3 0.242 0.029 8.295 0.000 0.242 0.102
## .B4 0.435 0.046 9.533 0.000 0.435 0.164
## .B5 0.230 0.028 8.234 0.000 0.230 0.100
## .I1 0.509 0.058 8.820 0.000 0.509 0.186
## .I2 0.328 0.041 7.994 0.000 0.328 0.145
## .I3 0.316 0.040 7.862 0.000 0.316 0.140
## .I4 0.838 0.082 10.239 0.000 0.838 0.359
## .A1 0.593 0.070 8.478 0.000 0.593 0.248
## .A2 1.045 0.113 9.213 0.000 1.045 0.310
## .A3 0.503 0.059 8.571 0.000 0.503 0.254
## .A4 1.361 0.134 10.140 0.000 1.361 0.457
## .A5 0.869 0.095 9.116 0.000 0.869 0.300
## .E1 0.717 0.075 9.584 0.000 0.717 0.195
## .E2 0.431 0.052 8.322 0.000 0.431 0.121
## .E3 0.478 0.056 8.492 0.000 0.478 0.127
## .E4 0.525 0.058 9.107 0.000 0.525 0.158
## .E5 0.575 0.061 9.429 0.000 0.575 0.182
## .T1 0.445 0.045 9.844 0.000 0.445 0.173
## .T2 0.496 0.051 9.743 0.000 0.496 0.163
## .T3 0.351 0.038 9.227 0.000 0.351 0.126
## .T4 0.348 0.038 9.056 0.000 0.348 0.117
## .T5 0.643 0.065 9.960 0.000 0.643 0.186
## .T6 0.301 0.035 8.490 0.000 0.301 0.095
## .Brand 1.000 0.662 0.662
## .Influencer 1.000 0.238 0.238
## Attractivity 1.000 1.000 1.000
## Expertise 1.000 1.000 1.000
## Vertrauen 1.000 1.000 1.000
##
## R-Square:
## Estimate
## B1 0.830
## B2 0.877
## B3 0.898
## B4 0.836
## B5 0.900
## I1 0.814
## I2 0.855
## I3 0.860
## I4 0.641
## A1 0.752
## A2 0.690
## A3 0.746
## A4 0.543
## A5 0.700
## E1 0.805
## E2 0.879
## E3 0.873
## E4 0.842
## E5 0.818
## T1 0.827
## T2 0.837
## T3 0.874
## T4 0.883
## T5 0.814
## T6 0.905
## Brand 0.338
## Influencer 0.7624.3.6 Ausgabe nur Ladungen
inspect(fit, what = "std")[["lambda"]]## Brand Inflnc Attrct Exprts Vertrn
## B1 0.911 0.000 0.000 0.000 0.000
## B2 0.936 0.000 0.000 0.000 0.000
## B3 0.948 0.000 0.000 0.000 0.000
## B4 0.914 0.000 0.000 0.000 0.000
## B5 0.949 0.000 0.000 0.000 0.000
## I1 0.000 0.902 0.000 0.000 0.000
## I2 0.000 0.924 0.000 0.000 0.000
## I3 0.000 0.927 0.000 0.000 0.000
## I4 0.000 0.801 0.000 0.000 0.000
## A1 0.000 0.000 0.867 0.000 0.000
## A2 0.000 0.000 0.831 0.000 0.000
## A3 0.000 0.000 0.864 0.000 0.000
## A4 0.000 0.000 0.737 0.000 0.000
## A5 0.000 0.000 0.837 0.000 0.000
## E1 0.000 0.000 0.000 0.897 0.000
## E2 0.000 0.000 0.000 0.938 0.000
## E3 0.000 0.000 0.000 0.934 0.000
## E4 0.000 0.000 0.000 0.917 0.000
## E5 0.000 0.000 0.000 0.905 0.000
## T1 0.000 0.000 0.000 0.000 0.910
## T2 0.000 0.000 0.000 0.000 0.915
## T3 0.000 0.000 0.000 0.000 0.935
## T4 0.000 0.000 0.000 0.000 0.940
## T5 0.000 0.000 0.000 0.000 0.902
## T6 0.000 0.000 0.000 0.000 0.9524.3.7 Ausgabe nur Pfadkoeffizienten
inspect(fit, what = "std")[["beta"]]## Brand Inflnc Attrct Exprts Vertrn
## Brand 0 0.582 0.000 0.000 0.000
## Influencer 0 0.000 0.442 0.048 0.506
## Attractivity 0 0.000 0.000 0.000 0.000
## Expertise 0 0.000 0.000 0.000 0.000
## Vertrauen 0 0.000 0.000 0.000 0.0004.3.8 Ausgabe Cronbachs Alpha und AVE (average variance extracted) für die Konstrukte
semTools::reliability(fit)## Brand Influencer Attractivity Expertise Vertrauen
## alpha 0.9698263 0.9367862 0.9125850 0.9638698 0.9722914
## omega 0.9698642 0.9381847 0.9130876 0.9643242 0.9728291
## omega2 0.9698642 0.9381847 0.9130876 0.9643242 0.9728291
## omega3 0.9692890 0.9378042 0.9104235 0.9644464 0.9731355
## avevar 0.8656284 0.7922392 0.6789615 0.8441257 0.85676734.3.9 Ausgabe der Interkorrelationsmatrix
lavInspect(fit, "cor.lv")## Brand Inflnc Attrct Exprts Vertrn
## Brand 1.000
## Influencer 0.582 1.000
## Attractivity 0.436 0.750 1.000
## Expertise 0.385 0.662 0.545 1.000
## Vertrauen 0.458 0.788 0.557 0.738 1.0004.3.10 Vollständiger Plot mit lavaanPlot
lavaanPlot(model=fit, coefs=T, cov=T, stand = T, stars = c ("covs", "latent","regress"),
edge_option=list(color="grey"))4.3.11 Berechnung der Scores pro Person für die einzelnen Konstrukte
scores <- predict(fit)
head(scores)## Brand Influencer Attractivity Expertise Vertrauen
## [1,] -2.4043931 -0.1651260 -1.2086711 1.60143719 -0.043553196
## [2,] -0.5825947 0.5627492 0.2286769 0.01815076 -0.002251716
## [3,] 1.6106453 1.5316043 0.2318923 1.01945989 0.881730763
## [4,] -0.3419586 3.0993704 1.4647338 1.72721872 1.814620206
## [5,] 1.0104828 0.5998556 1.3161763 0.20526640 0.072400003
## [6,] -1.9813272 0.3736186 -0.3875203 0.11490258 0.0023286374.3.12 Geschlecht als moderierende Variable
Geschlecht als moderierende Variable zwischen Influencer und Brand. D. h. es gibt die Annahme (Hypothese), dass es einen Interaktionseffekt zwischen Geschlecht und Influencer gibt.
Zunächst muss das Geschlecht als Faktor definiert werden:
data$Geschlecht = as.factor(data$Geschlecht)Als nächstes wird aus dem Geschlecht eine Dummyvariable mit 0/1 Codierung generiert
dummy<-dummy.code(data$Geschlecht) # ggf. das Paket psych nachladen
head(dummy)## weiblich maennlich
## [1,] 0 1
## [2,] 1 0
## [3,] 1 0
## [4,] 1 0
## [5,] 1 0
## [6,] 1 0Sodann wird das Produkt aus einem der Geschlechter-Dummys und der endogenen Variable auf Brand berechnet und dem finalen Datensatz hinzugefügt. Nachfolgende sind die beiden Spalten Geschlecht und die neue Interaktionsvariable zu sehen. Da die männliche Dummy für die Multiplikation ausgewählt wurde gibt es in der Interaktionsvariable nur Werte ungleich Null für die männlichen APN.
inter<-scores[,"Influencer"]*dummy[,"maennlich"]
data_mod = cbind(data, inter)
data_mod[1:10,c(1,28)]## Geschlecht inter
## 1 maennlich -0.16512600
## 2 weiblich 0.00000000
## 3 weiblich 0.00000000
## 4 weiblich 0.00000000
## 5 weiblich 0.00000000
## 6 weiblich 0.00000000
## 7 weiblich 0.00000000
## 8 maennlich -1.68832546
## 9 maennlich -0.01625029
## 10 weiblich 0.00000000Im Messmodell muss die Interatkionsvariable einer latenten Variable (hier Mod) zu gewiesen werden, bevor die Regressionsbeziehung auf Brand definiert werden kann.
semModel_IM_dummy <- "
# Measurement Model
Brand =~ B1 + B2 + B3 + B4 + B5
Influencer =~ I1 + I2 + I3 + I4
Attractivity =~ A1 + A2 + A3 + A4 + A5
Expertise =~ E1 + E2 + E3 + E4 + E5
Vertrauen =~ T1 + T2 + T3 + T4 + T5 + T6
Mod =~ inter
# regressions
Influencer ~ Attractivity + Expertise + Vertrauen
Brand ~ Influencer + Mod "
fit <- sem(semModel_IM_dummy , data=data_mod, estimator = "ml", std.lv=TRUE)
semPaths(fit, what="std", fade=F, residuals=F,
layout="tree2", structural=F, exoCov=F, nCharNodes=10, edge.label.cex=.8,
rotation = 2, sizeLat=10, nDigits = 3)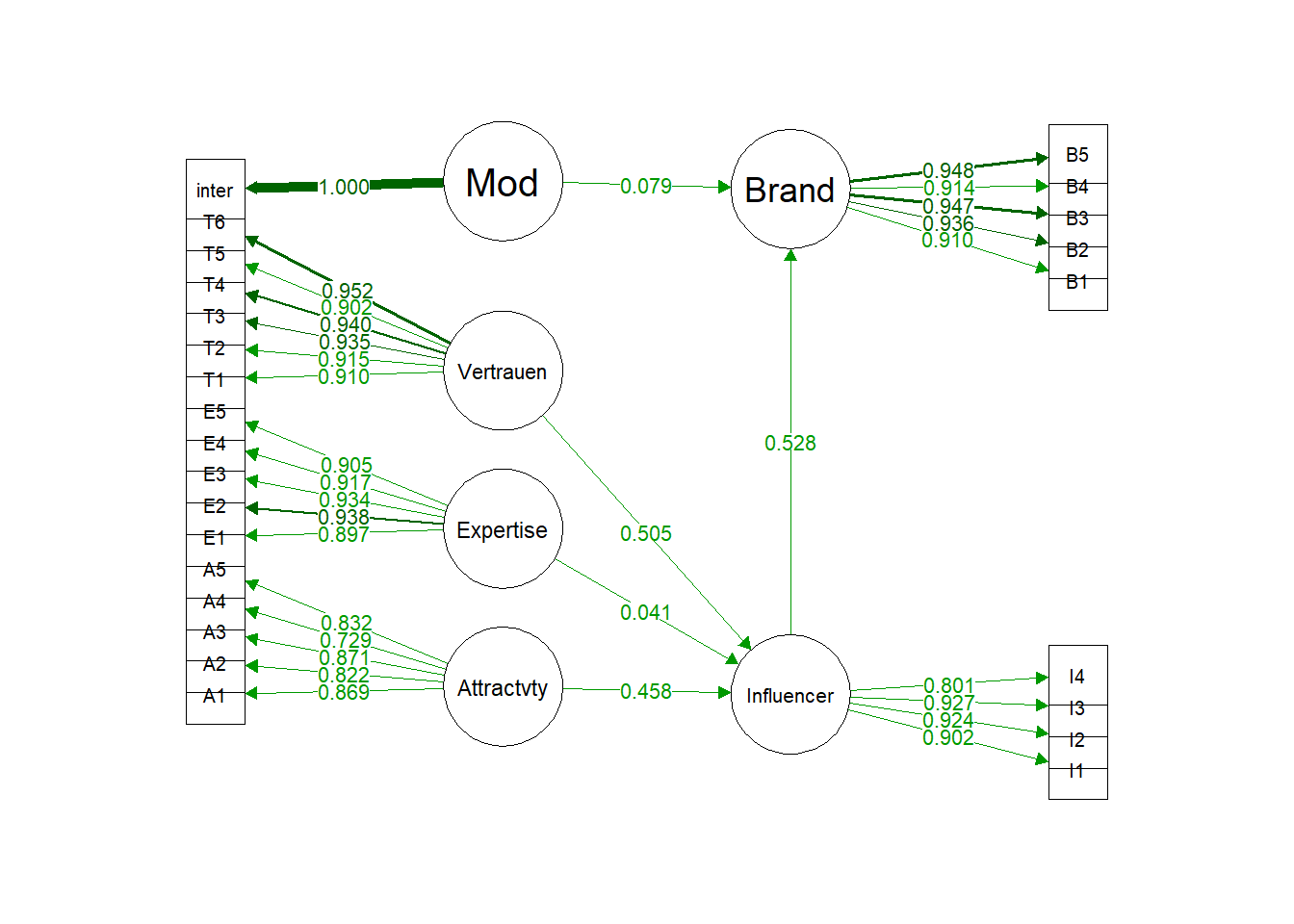
summary(fit, fit.measures=T, rsquare=T, standardized = T)## lavaan 0.6.17 ended normally after 56 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 62
##
## Number of observations 250
##
## Model Test User Model:
##
## Test statistic 522.463
## Degrees of freedom 289
## P-value (Chi-square) 0.000
##
## Model Test Baseline Model:
##
## Test statistic 8290.984
## Degrees of freedom 325
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.971
## Tucker-Lewis Index (TLI) 0.967
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -8637.910
## Loglikelihood unrestricted model (H1) -8376.678
##
## Akaike (AIC) 17399.820
## Bayesian (BIC) 17618.150
## Sample-size adjusted Bayesian (SABIC) 17421.605
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.057
## 90 Percent confidence interval - lower 0.049
## 90 Percent confidence interval - upper 0.065
## P-value H_0: RMSEA <= 0.050 0.075
## P-value H_0: RMSEA >= 0.080 0.000
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.051
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Brand =~
## B1 1.271 0.070 18.244 0.000 1.556 0.910
## B2 1.187 0.062 19.109 0.000 1.453 0.936
## B3 1.188 0.061 19.521 0.000 1.455 0.947
## B4 1.211 0.066 18.367 0.000 1.483 0.914
## B5 1.171 0.060 19.562 0.000 1.434 0.948
## Influencer =~
## I1 0.711 0.047 15.073 0.000 1.493 0.902
## I2 0.661 0.043 15.475 0.000 1.389 0.924
## I3 0.662 0.043 15.525 0.000 1.391 0.927
## I4 0.582 0.044 13.165 0.000 1.223 0.801
## Attractivity =~
## A1 1.345 0.079 17.036 0.000 1.345 0.869
## A2 1.509 0.097 15.592 0.000 1.509 0.822
## A3 1.226 0.072 17.094 0.000 1.226 0.871
## A4 1.258 0.096 13.099 0.000 1.258 0.729
## A5 1.415 0.089 15.875 0.000 1.415 0.832
## Expertise =~
## E1 1.717 0.094 18.213 0.000 1.717 0.897
## E2 1.773 0.090 19.694 0.000 1.773 0.938
## E3 1.812 0.093 19.561 0.000 1.812 0.934
## E4 1.671 0.088 18.938 0.000 1.671 0.917
## E5 1.610 0.087 18.483 0.000 1.610 0.905
## Vertrauen =~
## T1 1.459 0.078 18.697 0.000 1.459 0.910
## T2 1.598 0.085 18.883 0.000 1.598 0.915
## T3 1.563 0.080 19.634 0.000 1.563 0.935
## T4 1.621 0.082 19.815 0.000 1.621 0.940
## T5 1.677 0.091 18.427 0.000 1.677 0.902
## T6 1.697 0.084 20.273 0.000 1.697 0.952
## Mod =~
## inter 1.293 0.058 22.361 0.000 1.293 1.000
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Influencer ~
## Attractivity 0.962 0.124 7.749 0.000 0.458 0.458
## Expertise 0.085 0.118 0.720 0.472 0.041 0.041
## Vertrauen 1.060 0.143 7.394 0.000 0.505 0.505
## Brand ~
## Influencer 0.308 0.046 6.748 0.000 0.528 0.528
## Mod 0.097 0.080 1.211 0.226 0.079 0.079
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Attractivity ~~
## Expertise 0.544 0.048 11.240 0.000 0.544 0.544
## Vertrauen 0.556 0.047 11.767 0.000 0.556 0.556
## Mod 0.607 0.042 14.284 0.000 0.607 0.607
## Expertise ~~
## Vertrauen 0.738 0.031 23.984 0.000 0.738 0.738
## Mod 0.459 0.051 8.982 0.000 0.459 0.459
## Vertrauen ~~
## Mod 0.539 0.046 11.802 0.000 0.539 0.539
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .B1 0.502 0.052 9.611 0.000 0.502 0.172
## .B2 0.301 0.034 8.876 0.000 0.301 0.125
## .B3 0.242 0.029 8.299 0.000 0.242 0.103
## .B4 0.434 0.046 9.532 0.000 0.434 0.165
## .B5 0.229 0.028 8.228 0.000 0.229 0.100
## .I1 0.509 0.058 8.832 0.000 0.509 0.186
## .I2 0.328 0.041 8.009 0.000 0.328 0.145
## .I3 0.315 0.040 7.867 0.000 0.315 0.140
## .I4 0.837 0.082 10.243 0.000 0.837 0.359
## .A1 0.586 0.069 8.516 0.000 0.586 0.244
## .A2 1.093 0.116 9.397 0.000 1.093 0.325
## .A3 0.478 0.056 8.470 0.000 0.478 0.241
## .A4 1.394 0.136 10.216 0.000 1.394 0.468
## .A5 0.893 0.096 9.258 0.000 0.893 0.309
## .E1 0.717 0.075 9.585 0.000 0.717 0.196
## .E2 0.431 0.052 8.321 0.000 0.431 0.121
## .E3 0.478 0.056 8.490 0.000 0.478 0.127
## .E4 0.525 0.058 9.108 0.000 0.525 0.158
## .E5 0.575 0.061 9.428 0.000 0.575 0.182
## .T1 0.445 0.045 9.849 0.000 0.445 0.173
## .T2 0.498 0.051 9.754 0.000 0.498 0.163
## .T3 0.351 0.038 9.235 0.000 0.351 0.126
## .T4 0.347 0.038 9.062 0.000 0.347 0.117
## .T5 0.646 0.065 9.970 0.000 0.646 0.187
## .T6 0.300 0.035 8.494 0.000 0.300 0.094
## .inter 0.000 0.000 0.000
## .Brand 1.000 0.668 0.668
## .Influencer 1.000 0.227 0.227
## Attractivity 1.000 1.000 1.000
## Expertise 1.000 1.000 1.000
## Vertrauen 1.000 1.000 1.000
## Mod 1.000 1.000 1.000
##
## R-Square:
## Estimate
## B1 0.828
## B2 0.875
## B3 0.897
## B4 0.835
## B5 0.900
## I1 0.814
## I2 0.855
## I3 0.860
## I4 0.641
## A1 0.756
## A2 0.675
## A3 0.759
## A4 0.532
## A5 0.691
## E1 0.804
## E2 0.879
## E3 0.873
## E4 0.842
## E5 0.818
## T1 0.827
## T2 0.837
## T3 0.874
## T4 0.883
## T5 0.813
## T6 0.906
## inter 1.000
## Brand 0.332
## Influencer 0.7734.3.13 MGA mit lavaan
Im Gegensatz zu pls-pm biete lavaan keine Möglichkeit die Unterschiede der Pfadkoeffizienten zwischen den Gruppen (bei PLS-PM können nur zwei unterschieden werden) mit einem Signifikanztest (t-test) zu testen.
Lavaan hat trotzdem Vorteil bezüglich einer MGA:
Die Gruppen werden getrennt analysiert, egal wie viele Levels in der Gruppenvariable definiert sind. Also auch mehr als nur zwei.
Lavaan liefert für die MGA gleiche Ergebnisse wie für getrennte Analysen der Gruppen.
Bei PLS-PM habe ich festgestellt, dass unterschiedliche Ergebnisse berechnet werden und diese für mich nicht nachvollziehbar sind. Eine MGA liefert andere Ergebnisse als zwei getrennt durchgeführte Analysen mit je einer Gruppe. Leider antwortet der Autor des Pakets nicht auch meine Hinweise zu diesem Bug.
Aus diesem Grunde empfehle ich bei einer geplanten MGA immer die Analyse mit Lavaan durchzuführen, auch wenn keine Signifikanztests zwischen den Gruppen durchgeführt werden kann.
fit <- sem(semModel_IM, data=data, estimator = "ml", std.lv=TRUE, group = "Geschlecht")
semPaths(fit, what="std", fade=F, residuals=F,
layout="tree2", structural=T, exoCov=F, nCharNodes=10, edge.label.cex=.8,
rotation = 2, sizeLat=10, nDigits = 3, panelGroups = T,combineGroups = T)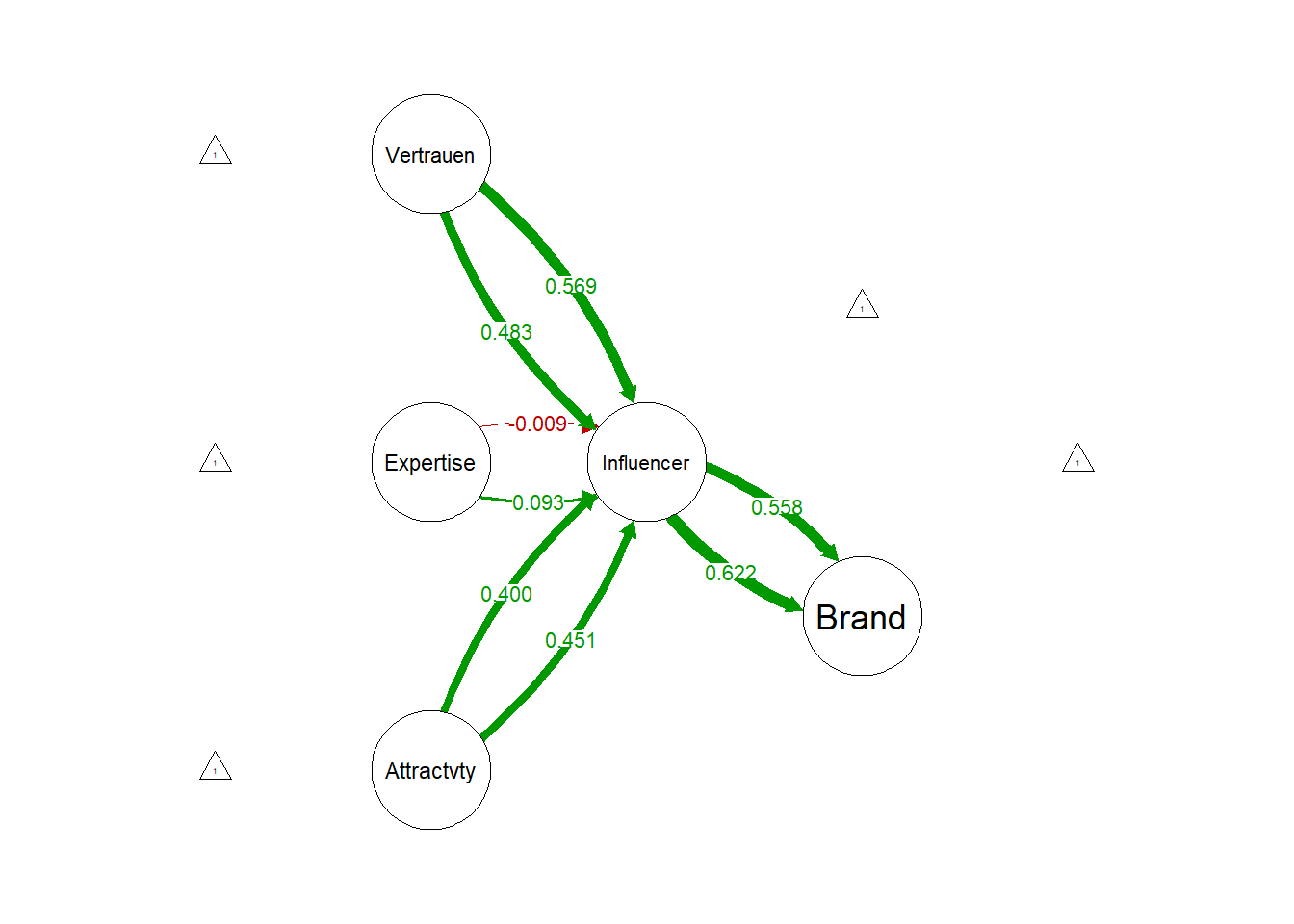
summary(fit, fit.measures=T, rsquare=T, standardized = T)## lavaan 0.6.17 ended normally after 64 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 164
##
## Number of observations per group:
## maennlich 97
## weiblich 153
##
## Model Test User Model:
##
## Test statistic 852.993
## Degrees of freedom 536
## P-value (Chi-square) 0.000
## Test statistic for each group:
## maennlich 392.694
## weiblich 460.299
##
## Model Test Baseline Model:
##
## Test statistic 8095.372
## Degrees of freedom 600
## P-value 0.000
##
## User Model versus Baseline Model:
##
## Comparative Fit Index (CFI) 0.958
## Tucker-Lewis Index (TLI) 0.953
##
## Loglikelihood and Information Criteria:
##
## Loglikelihood user model (H0) -8184.085
## Loglikelihood unrestricted model (H1) -7757.588
##
## Akaike (AIC) 16696.170
## Bayesian (BIC) 17273.689
## Sample-size adjusted Bayesian (SABIC) 16753.795
##
## Root Mean Square Error of Approximation:
##
## RMSEA 0.069
## 90 Percent confidence interval - lower 0.060
## 90 Percent confidence interval - upper 0.077
## P-value H_0: RMSEA <= 0.050 0.000
## P-value H_0: RMSEA >= 0.080 0.015
##
## Standardized Root Mean Square Residual:
##
## SRMR 0.063
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
##
## Group 1 [maennlich]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Brand =~
## B1 1.312 0.116 11.289 0.000 1.675 0.913
## B2 1.226 0.104 11.759 0.000 1.565 0.936
## B3 1.240 0.102 12.207 0.000 1.583 0.957
## B4 1.214 0.107 11.326 0.000 1.550 0.915
## B5 1.263 0.101 12.501 0.000 1.613 0.971
## Influencer =~
## I1 0.735 0.084 8.786 0.000 1.430 0.857
## I2 0.690 0.075 9.258 0.000 1.343 0.899
## I3 0.685 0.072 9.452 0.000 1.333 0.918
## I4 0.628 0.081 7.778 0.000 1.222 0.769
## Attractivity =~
## A1 1.411 0.128 10.996 0.000 1.411 0.891
## A2 1.381 0.153 9.016 0.000 1.381 0.784
## A3 1.349 0.133 10.145 0.000 1.349 0.847
## A4 1.083 0.144 7.535 0.000 1.083 0.689
## A5 1.445 0.147 9.855 0.000 1.445 0.832
## Expertise =~
## E1 1.606 0.139 11.536 0.000 1.606 0.906
## E2 1.802 0.144 12.519 0.000 1.802 0.949
## E3 1.774 0.151 11.733 0.000 1.774 0.915
## E4 1.670 0.142 11.773 0.000 1.670 0.917
## E5 1.608 0.146 10.982 0.000 1.608 0.880
## Vertrauen =~
## T1 1.464 0.127 11.508 0.000 1.464 0.904
## T2 1.529 0.139 10.984 0.000 1.529 0.879
## T3 1.505 0.125 12.087 0.000 1.505 0.930
## T4 1.663 0.139 11.967 0.000 1.663 0.925
## T5 1.556 0.148 10.516 0.000 1.556 0.856
## T6 1.668 0.135 12.379 0.000 1.668 0.942
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Influencer ~
## Attractivity 0.878 0.183 4.796 0.000 0.451 0.451
## Expertise 0.181 0.159 1.142 0.253 0.093 0.093
## Vertrauen 0.940 0.200 4.696 0.000 0.483 0.483
## Brand ~
## Influencer 0.408 0.076 5.400 0.000 0.622 0.622
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Attractivity ~~
## Expertise 0.392 0.092 4.244 0.000 0.392 0.392
## Vertrauen 0.465 0.086 5.426 0.000 0.465 0.465
## Expertise ~~
## Vertrauen 0.612 0.067 9.132 0.000 0.612 0.612
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .B1 4.216 0.186 22.637 0.000 4.216 2.298
## .B2 4.402 0.170 25.923 0.000 4.402 2.632
## .B3 4.278 0.168 25.470 0.000 4.278 2.586
## .B4 4.216 0.172 24.510 0.000 4.216 2.489
## .B5 4.289 0.169 25.415 0.000 4.289 2.581
## .I1 4.093 0.169 24.153 0.000 4.093 2.452
## .I2 4.258 0.152 28.065 0.000 4.258 2.850
## .I3 4.124 0.147 27.970 0.000 4.124 2.840
## .I4 4.608 0.161 28.551 0.000 4.608 2.899
## .A1 4.402 0.161 27.374 0.000 4.402 2.779
## .A2 3.619 0.179 20.235 0.000 3.619 2.055
## .A3 4.711 0.162 29.142 0.000 4.711 2.959
## .A4 3.598 0.159 22.560 0.000 3.598 2.291
## .A5 3.948 0.176 22.385 0.000 3.948 2.273
## .E1 2.897 0.180 16.091 0.000 2.897 1.634
## .E2 3.289 0.193 17.053 0.000 3.289 1.731
## .E3 3.186 0.197 16.181 0.000 3.186 1.643
## .E4 3.206 0.185 17.335 0.000 3.206 1.760
## .E5 3.423 0.185 18.454 0.000 3.423 1.874
## .T1 3.701 0.164 22.511 0.000 3.701 2.286
## .T2 3.392 0.176 19.217 0.000 3.392 1.951
## .T3 3.505 0.164 21.323 0.000 3.505 2.165
## .T4 3.557 0.183 19.471 0.000 3.557 1.977
## .T5 3.216 0.185 17.429 0.000 3.216 1.770
## .T6 3.443 0.180 19.158 0.000 3.443 1.945
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .B1 0.561 0.091 6.170 0.000 0.561 0.167
## .B2 0.346 0.059 5.829 0.000 0.346 0.124
## .B3 0.230 0.044 5.178 0.000 0.230 0.084
## .B4 0.468 0.076 6.150 0.000 0.468 0.163
## .B5 0.160 0.037 4.331 0.000 0.160 0.058
## .I1 0.739 0.128 5.787 0.000 0.739 0.265
## .I2 0.429 0.083 5.148 0.000 0.429 0.192
## .I3 0.332 0.071 4.661 0.000 0.332 0.157
## .I4 1.033 0.163 6.358 0.000 1.033 0.409
## .A1 0.519 0.111 4.669 0.000 0.519 0.207
## .A2 1.195 0.199 6.021 0.000 1.195 0.385
## .A3 0.715 0.132 5.439 0.000 0.715 0.282
## .A4 1.294 0.201 6.434 0.000 1.294 0.525
## .A5 0.931 0.165 5.625 0.000 0.931 0.308
## .E1 0.563 0.097 5.794 0.000 0.563 0.179
## .E2 0.361 0.078 4.656 0.000 0.361 0.100
## .E3 0.613 0.108 5.648 0.000 0.613 0.163
## .E4 0.530 0.094 5.615 0.000 0.530 0.160
## .E5 0.753 0.124 6.094 0.000 0.753 0.226
## .T1 0.479 0.080 5.982 0.000 0.479 0.183
## .T2 0.685 0.110 6.217 0.000 0.685 0.227
## .T3 0.356 0.064 5.556 0.000 0.356 0.136
## .T4 0.470 0.083 5.666 0.000 0.470 0.145
## .T5 0.882 0.139 6.365 0.000 0.882 0.267
## .T6 0.352 0.068 5.219 0.000 0.352 0.112
## .Brand 1.000 0.613 0.613
## .Influencer 1.000 0.264 0.264
## Attractivity 1.000 1.000 1.000
## Expertise 1.000 1.000 1.000
## Vertrauen 1.000 1.000 1.000
##
## R-Square:
## Estimate
## B1 0.833
## B2 0.876
## B3 0.916
## B4 0.837
## B5 0.942
## I1 0.735
## I2 0.808
## I3 0.843
## I4 0.591
## A1 0.793
## A2 0.615
## A3 0.718
## A4 0.475
## A5 0.692
## E1 0.821
## E2 0.900
## E3 0.837
## E4 0.840
## E5 0.774
## T1 0.817
## T2 0.773
## T3 0.864
## T4 0.855
## T5 0.733
## T6 0.888
## Brand 0.387
## Influencer 0.736
##
##
## Group 2 [weiblich]:
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Brand =~
## B1 1.216 0.086 14.144 0.000 1.466 0.907
## B2 1.145 0.077 14.916 0.000 1.380 0.936
## B3 1.126 0.075 14.999 0.000 1.357 0.939
## B4 1.196 0.083 14.337 0.000 1.441 0.914
## B5 1.087 0.074 14.767 0.000 1.311 0.930
## Influencer =~
## I1 0.718 0.058 12.452 0.000 1.350 0.915
## I2 0.660 0.053 12.551 0.000 1.242 0.921
## I3 0.683 0.055 12.535 0.000 1.285 0.920
## I4 0.594 0.056 10.627 0.000 1.116 0.803
## Attractivity =~
## A1 1.048 0.091 11.560 0.000 1.048 0.800
## A2 1.354 0.115 11.811 0.000 1.354 0.811
## A3 0.903 0.073 12.420 0.000 0.903 0.838
## A4 1.174 0.121 9.701 0.000 1.174 0.707
## A5 1.168 0.102 11.446 0.000 1.168 0.794
## Expertise =~
## E1 1.651 0.119 13.835 0.000 1.651 0.882
## E2 1.567 0.106 14.815 0.000 1.567 0.918
## E3 1.639 0.108 15.184 0.000 1.639 0.931
## E4 1.506 0.105 14.375 0.000 1.506 0.902
## E5 1.406 0.098 14.337 0.000 1.406 0.901
## Vertrauen =~
## T1 1.357 0.094 14.367 0.000 1.357 0.900
## T2 1.546 0.102 15.215 0.000 1.546 0.930
## T3 1.493 0.098 15.188 0.000 1.493 0.929
## T4 1.517 0.096 15.813 0.000 1.517 0.950
## T5 1.642 0.110 14.939 0.000 1.642 0.920
## T6 1.619 0.102 15.923 0.000 1.619 0.953
##
## Regressions:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Influencer ~
## Attractivity 0.752 0.142 5.289 0.000 0.400 0.400
## Expertise -0.017 0.159 -0.107 0.915 -0.009 -0.009
## Vertrauen 1.070 0.190 5.637 0.000 0.569 0.569
## Brand ~
## Influencer 0.358 0.057 6.281 0.000 0.558 0.558
##
## Covariances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## Attractivity ~~
## Expertise 0.515 0.066 7.825 0.000 0.515 0.515
## Vertrauen 0.537 0.063 8.518 0.000 0.537 0.537
## Expertise ~~
## Vertrauen 0.779 0.034 22.597 0.000 0.779 0.779
##
## Intercepts:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .B1 4.614 0.131 35.289 0.000 4.614 2.853
## .B2 4.654 0.119 39.038 0.000 4.654 3.156
## .B3 4.673 0.117 39.991 0.000 4.673 3.233
## .B4 4.497 0.127 35.282 0.000 4.497 2.852
## .B5 4.562 0.114 40.055 0.000 4.562 3.238
## .I1 5.261 0.119 44.078 0.000 5.261 3.563
## .I2 5.340 0.109 48.971 0.000 5.340 3.959
## .I3 5.124 0.113 45.367 0.000 5.124 3.668
## .I4 5.451 0.112 48.485 0.000 5.451 3.920
## .A1 5.654 0.106 53.375 0.000 5.654 4.315
## .A2 5.013 0.135 37.162 0.000 5.013 3.004
## .A3 5.810 0.087 66.726 0.000 5.810 5.395
## .A4 4.778 0.134 35.566 0.000 4.778 2.875
## .A5 5.248 0.119 44.166 0.000 5.248 3.571
## .E1 4.026 0.151 26.610 0.000 4.026 2.151
## .E2 4.575 0.138 33.169 0.000 4.575 2.682
## .E3 4.490 0.142 31.547 0.000 4.490 2.550
## .E4 4.379 0.135 32.461 0.000 4.379 2.624
## .E5 4.693 0.126 37.198 0.000 4.693 3.007
## .T1 4.536 0.122 37.199 0.000 4.536 3.007
## .T2 4.281 0.134 31.850 0.000 4.281 2.575
## .T3 4.418 0.130 34.003 0.000 4.418 2.749
## .T4 4.379 0.129 33.926 0.000 4.379 2.743
## .T5 4.203 0.144 29.145 0.000 4.203 2.356
## .T6 4.359 0.137 31.754 0.000 4.359 2.567
##
## Variances:
## Estimate Std.Err z-value P(>|z|) Std.lv Std.all
## .B1 0.466 0.063 7.421 0.000 0.466 0.178
## .B2 0.269 0.040 6.698 0.000 0.269 0.124
## .B3 0.247 0.037 6.584 0.000 0.247 0.118
## .B4 0.408 0.056 7.284 0.000 0.408 0.164
## .B5 0.266 0.039 6.882 0.000 0.266 0.134
## .I1 0.357 0.055 6.495 0.000 0.357 0.164
## .I2 0.277 0.044 6.292 0.000 0.277 0.152
## .I3 0.301 0.048 6.326 0.000 0.301 0.154
## .I4 0.688 0.086 7.969 0.000 0.688 0.356
## .A1 0.619 0.087 7.110 0.000 0.619 0.360
## .A2 0.951 0.137 6.967 0.000 0.951 0.342
## .A3 0.345 0.053 6.556 0.000 0.345 0.297
## .A4 1.382 0.176 7.835 0.000 1.382 0.501
## .A5 0.797 0.111 7.170 0.000 0.797 0.369
## .E1 0.777 0.103 7.527 0.000 0.777 0.222
## .E2 0.457 0.067 6.865 0.000 0.457 0.157
## .E3 0.413 0.064 6.464 0.000 0.413 0.133
## .E4 0.517 0.072 7.217 0.000 0.517 0.186
## .E5 0.459 0.063 7.242 0.000 0.459 0.188
## .T1 0.433 0.055 7.897 0.000 0.433 0.190
## .T2 0.374 0.050 7.463 0.000 0.374 0.135
## .T3 0.354 0.047 7.482 0.000 0.354 0.137
## .T4 0.249 0.036 6.884 0.000 0.249 0.098
## .T5 0.486 0.064 7.637 0.000 0.486 0.153
## .T6 0.262 0.039 6.729 0.000 0.262 0.091
## .Brand 1.000 0.688 0.688
## .Influencer 1.000 0.283 0.283
## Attractivity 1.000 1.000 1.000
## Expertise 1.000 1.000 1.000
## Vertrauen 1.000 1.000 1.000
##
## R-Square:
## Estimate
## B1 0.822
## B2 0.876
## B3 0.882
## B4 0.836
## B5 0.866
## I1 0.836
## I2 0.848
## I3 0.846
## I4 0.644
## A1 0.640
## A2 0.658
## A3 0.703
## A4 0.499
## A5 0.631
## E1 0.778
## E2 0.843
## E3 0.867
## E4 0.814
## E5 0.812
## T1 0.810
## T2 0.865
## T3 0.863
## T4 0.902
## T5 0.847
## T6 0.909
## Brand 0.312
## Influencer 0.7174.3.14 Tipps zur Dokumentation
Um die Ergebnisse einer Datenanalyse mit lavaan zu dokumentieren, empfehle ich folgende Schritte:
- summary anschauen und alle Items mit multiplem r2 < 0,2 aus dem Modell eliminieren. Siehe hierzu Hooper et al. 2008
- Validität und Reliabilität überprüfen
- Globale Gütekriterien aus der summery (CFI, TLI, RMSEA und SRMR) in Bezug auf die Schwellenwerte überprüfen Auch hier kann Hooper et al. 2008 herangezogen werden
- R2 der endogenen Konstrukte (kann auch ins Modell mit geschrieben werden)
Fühlen Sie sich frei bei der Interpretation alle Gütekriterien die für Sie relevante Literatur zu zitieren.
Eine mögliche Literaturquelle mit ausführlichen Erklärungen bei Strukturgleichungsmodellierung ist Weiber, R., & Mühlhaus, D. (2014). Strukturgleichungsmodellierung.
Die Schwellenwerte für die Gütekriterien und die Quellen sind in den Tabellen unten zusammengefasst.
4.3.15 Schätzverfahren
Verschiedene Schätzmethoden gehen von unterschiedlichen Annahmen aus. Hierunter befinden sich mit der Methode der Instrumentalvariablen (IV) und der Zweistufenmethode der kleinsten Quadrate (TSLS) zwei nicht-iterative Verfahren, deren Schätzwerte sowohl als endgültige Modellschätzer als auch als Startwerte für iterative Verfahren verwendet werden können. IV und TSLS sind einerseits zwar relativ robust gegenüber Fehlspezifikationen, bieten andererseits aber nicht die Möglichkeit, Teststatistiken zu berechnen.
Daher werden meist iterative Verfahren angewandt, die alle Informationen der Korrelationsmatrix simultan verwenden und Teststatistiken berechnen. Das Programm bietet folgende iterative Schätzverfahren an:
- Maximum-Likelihood-Methode (ML)
- Methode der ungewichteten kleinsten Quadrate (ULS)
- Methode der verallgemeinerten kleinsten Quadrate (GLS)
- Methode der allgemein gewichteten kleinsten Quadrate (WLS)
- Methode der diagonal gewichteten kleinsten Quadrate (DWLS)
Die GLS- und ML-Methoden setzen normalverteilte Ausgangsvariablen voraus, was in vorliegenden Datensätzen bei Umfragen oft nicht gegeben ist.
Die drei anderen iterativen Verfahren setzen hingegen keine Multi-Normalverteilung der beobachteten Variablen voraus. Für die ULS-Methode ist die Normalverteilungsannahme aber dennoch bedeutsam, da Standardfehler, t-Werte, standardisierte Residuen und der Chi-Quadrat-Test nur dann zur Interpretation herangezogen werden dürfen, wenn diese Annahme erfüllt ist.
Besondere Anforderungen an den Stichprobenumfang stellen die WLS- und DWLS-Methode in Abhängigkeit von der Anzahl der Indikatoren.
Trotz der jeweils angegebenen Einschränkungen kann ein Vergleich der verschiedenen Ergebnisse dieser Methoden wertvolle Hinweise auf die Stabilität der Messung liefern.
4.3.16 Güte des Gesamtmodells
Zur Prüfung der Anpassungsgüte der Modellstruktur an die empirischen Daten lassen sich viele verschiedene Größen verwenden. Homburg/Baumgartner (1995) untergliedern die gängigsten Anpassungsmaße anhand ihrer Eigenheiten in verschiedene Kategorien. Nur eine Gegenüberstellung mehrerer Maßgrößen aus verschiedenen solcher Klassen erlaubt eine recht umfassende Einschätzung der tatsächlichen Güte des Modells, da ein Modell selbst dann nicht automatisch abzulehnen ist, wenn ein einzelnes Anpassungsmaß unterschritten wird.
Eine sehr gute Übersicht liefert auch
Aus diesen Überlegungen heraus könne die folgenden Anpassungsmaße zur Anwendung herangezogen werden:
| Anpassungsmaß | zu erfüllendes Kriterium | Kurz-Erläuterung |
|---|---|---|
| Goodness-of-fit index (GFI) | ≥ 0,9 | Anteil der Varianzen und Kovarianzen in der Matrix S, der durch das Modell erklärt wird. Ein Wert von 1 entspricht einer perfekten Anpassung des Modells an die Daten. |
| Standardized root mean residual (SRMR) | ≤ 0,05 | Durchschnittliche Größe der Residuen zwischen Elementen der empirischen Kovarianzmatrix und denen der vom Modell reproduzierten Kovarianzmatrix. |
| Adjusted GFI (AGFI) | ≥ 0,9 | Wie GFI, berücksichtigt aber auch die Zahl der Freiheitsgrade. |
| Normed-fit-index (NFI) | ≥ 0,9 | Misst die Verbesserung der Anpassungsgüte von einem Nullmodell zum relevanten Modell. |
| Comparative-fit-index (CFI) | ≥ 0,9 | Wie NFI, berücksichtigt aber auch die Zahl der Freiheitsgrade. |
Die einzelnen Gütekriterien können Sie auch durch fogenden Befehl ausgeben (gebiebig anpassbar):
fitMeasures(fit, c("chisq", "df", "rmsea", "gfi", "agfi", "rmr", "srmr", "nfi", "nnfi", "cfi" ))## chisq df rmsea gfi agfi rmr srmr nfi nnfi cfi
## 852.993 536.000 0.069 0.919 0.894 0.166 0.063 0.895 0.953 0.9585 Prüfkriterien SEM-Analyse
Zunächst ist die Unterscheidung zwischen reflektiven und formativen Messmodellen wichtig, da sie unterschiedlich überprüft werden. Als Messmodell wird ein Konstrukt bestehend aus mehreren messbaren Variablen (Indikatoren, Items) und einer latenten (nicht messbaren) Variable bezeichnet. Das Messmodell ist formativ, wenn alle Indikatoren auf die latente Variable wirken. Wenn also die Pfeile alle in Richtung der latenten Variable zeigen. Als reflektiv wird das Messmodell bezeichnet, wenn die latente Variable auf die gemessenen Indikatoren wirkt. In diesem Fall gehen die Pfeile im Modell von der latenten Variable zu den einzelnen Indikatoren.
Wenn einzelne Indikatoren schlechte Werte zeigen, so können diese schrittweise ausgeschlossen werden und das Modell neu berechnet werden. Variablen aus formativen Messmodellen sollten nur herausgenommen werden, wenn diese Entscheidung inhaltlich sehr gut argumentiert werden kann.
| Prüfung der reflektiven Messmodelle: | Erläuterungen und Prüfkriterien |
|---|---|
| Cronbachs Alpha und Item-to-Total-Korrelation |
α ≥ 0,7 für Konstrukte mit vier oder mehr Indikatoren α ≥ 0,6 für Konstrukte mit drei Indikatoren α ≥ 0,5 für Konstrukte mit zwei Indikatoren (vgl. Ohlwein, 1999, S. 224) Bei Unterschreitung der Schwellenwerte für Cronbachs Alpha kann mittels der Item-to-Total-Korrelation entschieden werden, ob sich die Reliabilität des Messmodells durch Ausschluss des Indikators mit der geringsten Item-to-Total-Korrelation verbessern lässt (vgl. Homburg/Rudolph, 1998, S. 253). |
| Indikatorreliabilität für jedes Item des Messmodells: Ladung und Signifikanz | Ladung ≥ 0,7 (ggfs. ≥ 0,5) (vgl. Chin, 1998) t-Wert > 1,96 (zweiseitig) bzw. 1,65 (einseitig) bei 5%-Niveau ; > 1,65 (zweiseitig) bzw. 1,28 (einseitig) bei 10%-Niveau |
| Konvergenzkriterien für das Messmodell: AVE (durchschnittlich erfasste Varianz, DEV) und Composite Reliability (Konstruktreliabilität, interne Konsistenz) | AVE > 0,5 Composite Reliability > 0,6 (vgl. Homburg/Baumgartner, 1998, S. 361; Bagozzi/Yi, 1988, S. 82). |
| Diskriminanzvalidität: Fornell-Larcker Kriterium (für das Messmodell) und Kreuzladungen (für jedes Item des Messmodells) | Fornell-Larcker-Kriterium: In dieser Tabelle sind die Einträge unterhalb der Diagonalen die Korrelationen. Diese sollen alle kleiner als die Wurzel aus der AVE (Werte auf der Hauptdiagonalen) sein (vgl. Homburg et al., 2008, S. 287; Fornell/Larcker, 1981, S. 46). Jede Variable (Item) soll auf ihr eigenes Konstrukt (Messmodell) deutlich höher laden als auf alle anderen Konstrukte (vgl. Chin, 1998, S. 321 f.). |
| Prüfung der formativen Messmodelle: | Erläuterungen und Prüfkriterien |
|---|---|
| Indikatorreliabilität für jedes Item: Signifikanz der Gewichte (Indikatorrelevanz und Indikatorsignifikanz) | Gewichte > 0,2 (vgl. Lohmüller, 1989, S. 60 f.; Chin, 1998, S. 324 f.). t-Wert > 1,96 (zweiseitig) bzw. 1,65 (einseitig) bei 5%-Niveau ; > 1,65 (zweiseitig) bzw. 1,28 (einseitig) bei 10%-Niveau |
| Diskriminanzvalidität: Konstruktkorrelation | Korrelation des formativen Konstrukts mit den übrigen Konstrukten soll kleiner als 0,9 sein. |
| Abwesenheit von Multikollinearität: | Der VIF sollte nahe 1 liegen, dann liegt keine Multikollinearität vor, und nicht größer als 10 (5) werden (vgl. z. B. Diamantopoulos/Winklhofer, 2001, S. 272). |
| Prüfung des inneren Modells: | Erläuterungen und Prüfkriterien |
|---|---|
| Wirkstärke und Signifikanz der Pfadkoeffizienten zwischen den latenten Konstrukten | Pfadkoeffizienten > 0,2 (vgl. Lohmüller, 1989, S. 60 f.; Chin, 1998, S. 324 f.). t-Wert > 1,96 (zweiseitig) bzw. 1,65 (einseitig) bei 5%-Niveau ; > 1,65 (zweiseitig) bzw. 1,28 (einseitig) bei 10%-Niveau |
| erklärte Varianz R² für endogene Konstrukte | R² ≥ 0,67 gilt als substanziell, R² ≥ 0,33 gilt als durchschnittlich und R² ≥ 0,19 gilt als schwach (vgl. Chin 1998, S. 325). |
| Prognoserelevanz Q² für endogene Konstrukte | Q² > 0 |
| Multikollinearität | Abwesenheit von Multikollinearität bei jedem endogenen Konstrukt, welches durch zwei oder mehr latente Größen bestimmt wird. Die Überprüfung kann ebenfalls über den VIF erfolgen, wobei ein kritischer Wert von 10 (5) nicht überschritten werden sollte (vgl. Huber et al., 2007, S. 108 f.). |
6 Literatur
- Bagozzi, R. P.; Yi, Y. (1988): On the Evaluation of Structural Equation Models, in: Journal of the Academy of Marketing Science, Vol. 16, No. 1, S. 74 – 94.
- Chris Chapman, Elea McDonnell Feit (2015): R for Marketing Research and Analytics
- Diamantopoulos, A.; Riefler, P. (2008): Formative Indikatoren: Einige Anmerkungen zu ihrer Art, Validität und Multikollinearität, in: ZFB Zeitschrift für Betriebswirtschaft, 78. Jg., Nr. 11, S. 1183 1196.
- Chin, W. W. (1998): The Partial Least Squares Approach to Structural Equation Modeling, in: Marcoulides, G.A. (Hrsg.), Modern Methods for Business Research, London, S. 295 – 336.
- Fornell, C.; Larcker, D. F. (1981): Evaluating Structural Equation Models with Unobservable Variables and Measurement Error, in: Journal of Marketing Research, Vol. 18, No. 1, S. 39 – 50.
- Homburg, C. und H. Baumgartner (1995): Die Kausalanalyse als Instrument der Marketingforschung, in: Zeitschrift für Betriebswirtschaft, Heft 10, S. 1091-1108
- Homburg, C.; Rudolph, B. (1998): Die Kausalanalyse als Instrument zur Messung der Kundenzufriedenheit in Industriegütermärkten, in: Hildebrandt, L.; Homburg, C. (Hrsg.), Die Kausalanalyse, Stuttgart, S. 237 – 264.
- Huber, F.; Herrmann, A.; Meyer, F.; Vogel, J.; Vollhardt, K. (2007): Kausalmodellierung mit Partial Least Squares, Wiesbaden.
- Ohlwein, M. (1999): Märkte für gebrauchte Güter, Wiesbaden.