Dimensionsreduktion
1 Dimensionsreduktion
Datensätze in den Sozialwissenschaften, und damit auch in der Wirtschaftspsychologie, haben oft viele Variablen - oder auch Dimensionen - und es ist vorteilhaft, diese auf eine kleinere Anzahl von Variablen (oder Dimensionen) zu reduzieren. Zusammenhänge zwischen verschiedenen Dimensionen oder Unterschiede zwischen verschiedenen Gruppen bezüglich einer oder mehrerer Dimensionen (z. B. bei Experimenten) können so klarer und einfacher identifiziert werden. Dimensionen mit konkreten Sachverhalten werden in der Sprache der Wissenschaft häufig als Konstrukte bezeichnet.
Konstrukte stellen in den Sozialwissenschaften gedankliche bzw. theoretische Sachverhalt dar, die nicht direkt beobachtbar und damit nicht direkt messbar sind. Nehmen wir beispielsweise an, es soll das Konstrukt Anerkennung im Rahmen einer sozialwissenschaftlichen Studie gemessen werden. Dabei gibt es zunächst zwei Fragestellungen:
- Was bedeutet Anerkennung?
- Wie wird Anerkennung gemessen?
Liest man bei Wikipediea diesen Begriff nach, kommt folgende Antwort: “Anerkennung bedeutet die Erlaubnis einer Person oder einer Gruppe gegenüber einer anderen Person, Gruppe oder Institution, sich mit ihren derzeitigen spezifischen Eigenschaften an der Kommunikation, an Entscheidungsprozessen oder anderen gesellschaftlichen Prozessen zu beteiligen. Der Begriff Anerkennung wird auch als Synonym für Akzeptanz, Lob oder Respekt verwendet.” Gut, wir kennen nun die Bedeutung von Anerkennung, aber wir wissen immer noch nicht, wie wir Anerkennung messen können. Da die Suche nach Anerkennung in der Psychologie kein neues Konstrukt darstellt, sondern schon vielfach gemessen wurde, müssen wir nur in bisherigen Forschungsergebnissen nachlesen. Dies führt unweigerlich dazu, dass wir auf bisherige Forschungen stoßen, die das Konstrukt Anerkennung als ein multidimensionales Konstrukt definieren und mit mehr als einem Item (Indikator) messen. Mehr zur Messung von Anerkennung weiter unten im Datenbeispiel. D. h. der Sachverhalt Anerkennung wird aus anderen, messbaren Sachverhalten (Indikatoren) messbar gemacht. Der Prozess des „Messbar machens“ heißt Operationalisierung. Mehr zur Operationalisierung von Anerkennung und anderen Konstrukten betrachten wir weiter untern im Datenbeispiel.
In diesem Kapitel betrachten wir zwei gängige Methoden, um die Komplexität von multivarianten, metrischen Daten zu reduzieren, indem wir die Anzahl der Dimensionen in den Daten reduzieren.
- Die Hauptkomponentenanalyse (PCA) versucht, unkorrelierte Linearkombinationen zu finden, die die maximale Varianz in den Daten erfassen. Die PCA beinhaltet also das Extrahieren von linearen Zusammenhängen der beobachteten Variablen.
- Die Exploratorische Faktorenanalyse (EFA) versucht, die Varianz auf Basis einer kleinen Anzahl von Dimensionen zu modellieren, während sie gleichzeitig versucht, die Dimensionen in Bezug auf die ursprünglichen Variablen interpretierbar zu machen. Es wird davon ausgegangen, dass die Daten einem Faktoren Modell entsprechen, bei der die beobachteten Korrelationen auf
latenteFaktoren zurückführen. Mit der EFA wird nicht die gesamte Varianz erklärt.
In der Psychologie werden diese beiden Methoden oft in der Konstruktion von mehrstufigen Tests angewendet, um festzustellen, welche Items auf welche Konstrukte laden. Sie ergeben in der Regel ähnliche inhaltliche Schlussfolgerungen. Dies erklärt, warum einige Statistik-Software-Programme beide Methoden zusammenpacken. So wird die PCA als Standard-Extraktionsmethode in den SPSS-Faktoranalyse-Routinen verwendet. Dies führt zweifellos zu einer gewissen Verwirrung über die Unterscheidung zwischen den beiden Methoden. Die EFA wird oft als Common Factor Analysis oder principal axis factoring (Hauptachsenanalyse) bezeichnet. EFA verwendet eine Vielzahl von Optimierungsroutinen und das Ergebnis, im Gegensatz zu PCA, hängt von der verwendeten Optimierungsroutine und Ausgangspunkten für diese Routinen ab. Es gibt also keine einzigartige Lösung bei der EFA.
Eine einfache Faustregel für die Entscheidung zwischen diesen beiden Methoden:
- Führe die PCA durch, wenn die korrelierten beobachteten Variablen einfach auf einen kleineren Satz von wichtigen unabhängigen zusammengesetzten Variablen reduziert werden soll.
- Führe die EFA durch, wenn ein theoretisches Modell von latenten Faktoren zugrunde liegt, dass die beobachtete Variablen verursacht.
1.1 Gründe für die Notwendigkeit der Datenreduktion
- Im technischen Sinne der Dimensionsreduktion können wir statt Variablen-Sets die Faktor-/ Komponentenwerte verwenden (z. B. für Mittelwertvergleiche zwischen Experimental- und Kontrollgruppe, Regressionsanalyse und Clusteranalyse).
- Wir können Unsicherheit verringern. Wenn wir glauben, dass ein Konstrukt nicht eindeutig messbar ist, dann kann mit einem Variablen-Set die Unsicherheit reduziert werden.
- Wir können den Aufwand bei der Datenerfassung vereinfachen, indem wir uns auf Variablen konzentrieren, von denen bekannt ist, dass sie einen hohen Beitrag zum interessierenden Faktor/ Komponente leisten. Wenn wir feststellen, dass einige Variablen für einen Faktor nicht wichtig sind, können wir sie aus dem Datensatz eliminieren.
1.2 Benötigte Pakete
Pakete, die für diese Datenanalyse benötigt werden, müssen vorher einmalig in R installiert werden.
# install.packages("corrplot")
# install.packages("gplots")
# install.packages("nFactors")2 Daten
Wir untersuchen die Dimensionalität mittels einer auf 1000 Fälle reduzierten Zufallsauswahl von 15 Variablen zur Messung der grundlegenden Wertorientierungen von Menschen. Die Daten wurden im Sommersemester 2017 von FOM Studierenden im ersten Semester an der FOM bundesweit erhoben. Die Variablen zu Wertorientierungen wurden ursprüngliche aus dem 40-Item-Set des «Portraits Value Questionnaire» (PVQ) von Schwartz adaptiert und durch die Studien an der FOM seit 2014 stufenweise bis auf 15 relevante Variablen reduziert. Alle Variablen wurden auf einer Skala von 1 bis 7 (wobei 1 am wenigsten und 7 am meisten zutrifft) abgefragt.
Das Einlesen der Daten erfolgt mit dem Befehl read.csv2.
Werte <- read.csv2("https://osf.io/teymq/download", encoding="UTF-8")Wir überprüfen zuerst die Struktur des Datensatzes, die ersten 6 Zeilen und die Zusammenfassung.
str(Werte)## 'data.frame': 1000 obs. of 15 variables:
## $ Spaß : int 6 3 2 7 3 5 7 5 4 5 ...
## $ Freude : int 6 7 7 7 4 5 5 5 4 5 ...
## $ Aufregung : int 7 3 3 7 3 5 5 5 3 3 ...
## $ Führung : int 6 1 6 4 4 4 3 3 2 2 ...
## $ Entscheidung : int 6 1 6 3 4 3 4 3 1 2 ...
## $ Religiösität : int 2 7 4 1 5 1 3 3 3 1 ...
## $ Respekt : int 5 7 7 7 2 5 6 3 4 5 ...
## $ Demut : int 4 3 6 3 4 3 4 2 2 5 ...
## $ Gefahrenvermeidung: int 6 7 7 2 7 3 4 5 6 5 ...
## $ Sicherheit : int 6 7 7 6 7 4 6 6 7 4 ...
## $ Ordentlichkeit : int 6 7 3 3 6 5 6 7 3 7 ...
## $ Unabhängigkeit : int 6 7 7 5 3 7 5 6 2 5 ...
## $ Zuhören : int 5 6 1 3 3 5 5 4 5 6 ...
## $ Umweltbewusstsein : int 4 7 1 7 6 5 7 6 6 5 ...
## $ Interesse : int 7 6 7 5 2 7 7 6 7 7 ...head(Werte)## Spaß Freude Aufregung Führung Entscheidung Religiösität Respekt Demut
## 1 6 6 7 6 6 2 5 4
## 2 3 7 3 1 1 7 7 3
## 3 2 7 3 6 6 4 7 6
## 4 7 7 7 4 3 1 7 3
## 5 3 4 3 4 4 5 2 4
## 6 5 5 5 4 3 1 5 3
## Gefahrenvermeidung Sicherheit Ordentlichkeit Unabhängigkeit Zuhören
## 1 6 6 6 6 5
## 2 7 7 7 7 6
## 3 7 7 3 7 1
## 4 2 6 3 5 3
## 5 7 7 6 3 3
## 6 3 4 5 7 5
## Umweltbewusstsein Interesse
## 1 4 7
## 2 7 6
## 3 1 7
## 4 7 5
## 5 6 2
## 6 5 7summary(Werte)## Spaß Freude Aufregung Führung
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:4.000 1st Qu.:4.000 1st Qu.:3.000 1st Qu.:2.000
## Median :5.000 Median :5.000 Median :4.000 Median :4.000
## Mean :5.233 Mean :5.123 Mean :4.179 Mean :3.612
## 3rd Qu.:7.000 3rd Qu.:6.000 3rd Qu.:5.000 3rd Qu.:5.000
## Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
## Entscheidung Religiösität Respekt Demut
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:2.000 1st Qu.:1.000 1st Qu.:4.000 1st Qu.:2.000
## Median :4.000 Median :2.000 Median :5.000 Median :4.000
## Mean :3.714 Mean :2.955 Mean :4.783 Mean :3.684
## 3rd Qu.:5.000 3rd Qu.:4.000 3rd Qu.:6.000 3rd Qu.:5.000
## Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
## Gefahrenvermeidung Sicherheit Ordentlichkeit Unabhängigkeit
## Min. :1.000 Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:4.000 1st Qu.:5.000 1st Qu.:4.000 1st Qu.:5.000
## Median :5.000 Median :6.000 Median :6.000 Median :6.000
## Mean :4.996 Mean :5.651 Mean :5.198 Mean :5.556
## 3rd Qu.:6.000 3rd Qu.:7.000 3rd Qu.:6.000 3rd Qu.:7.000
## Max. :7.000 Max. :7.000 Max. :7.000 Max. :7.000
## Zuhören Umweltbewusstsein Interesse
## Min. :1.000 Min. :1.000 Min. :1.000
## 1st Qu.:4.000 1st Qu.:4.000 1st Qu.:4.000
## Median :5.000 Median :5.000 Median :6.000
## Mean :5.031 Mean :4.894 Mean :5.244
## 3rd Qu.:6.000 3rd Qu.:6.000 3rd Qu.:6.000
## Max. :7.000 Max. :7.000 Max. :7.000Wir sehen in der summary (), dass die Bereiche der Bewertungen für jede Variable 1-7 sind. In str() sehen wir, dass die Bewertungen als numerisch (Integer, also ganzzahlig) eingelesen wurden. Die Daten sind somit richtig formatiert.
3 Neuskalierung der Daten
In vielen Fällen ist es sinnvoll, Rohdaten neu zu skalieren. Dies wird üblicherweise als Standardisierung, Normierung, oder Z Scoring/Transformation bezeichnet. Als Ergebnis ist der Mittelwert aller Variablen über alle Beobachtungen dann 0. Da wir hier gleiche Skalenstufen haben, ist ein Skalieren nicht unbedingt notwendig, wir führen es aber trotzdem durch.
Ein einfacher Weg, alle Variablen im Datensatz auf einmal zu skalieren ist der Befehl scale(). Da wir die Rohdaten nie ändern wollen, weisen wir die Rohwerte zuerst einem neuen Dataframe Werte.sc zu und skalieren anschließend die Daten. Wir skalieren in unserem Datensatz alle Variablen.
Werte.sc<- scale(Werte)
summary(Werte.sc)## Spaß Freude Aufregung Führung
## Min. :-2.8417 Min. :-2.80273 Min. :-1.8739 Min. :-1.4505
## 1st Qu.:-0.8277 1st Qu.:-0.76339 1st Qu.:-0.6950 1st Qu.:-0.8952
## Median :-0.1564 Median :-0.08361 Median :-0.1055 Median : 0.2155
## Mean : 0.0000 Mean : 0.00000 Mean : 0.0000 Mean : 0.0000
## 3rd Qu.: 1.1862 3rd Qu.: 0.59617 3rd Qu.: 0.4840 3rd Qu.: 0.7708
## Max. : 1.1862 Max. : 1.27595 Max. : 1.6629 Max. : 1.8814
## Entscheidung Religiösität Respekt Demut
## Min. :-1.5357 Min. :-0.9976 Min. :-2.2525 Min. :-1.6078
## 1st Qu.:-0.9698 1st Qu.:-0.9976 1st Qu.:-0.4662 1st Qu.:-1.0087
## Median : 0.1618 Median :-0.4873 Median : 0.1292 Median : 0.1893
## Mean : 0.0000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
## 3rd Qu.: 0.7277 3rd Qu.: 0.5332 3rd Qu.: 0.7246 3rd Qu.: 0.7883
## Max. : 1.8593 Max. : 2.0640 Max. : 1.3200 Max. : 1.9863
## Gefahrenvermeidung Sicherheit Ordentlichkeit Unabhängigkeit
## Min. :-2.528060 Min. :-3.2993 Min. :-2.6748 Min. :-3.4336
## 1st Qu.:-0.630117 1st Qu.:-0.4618 1st Qu.:-0.7633 1st Qu.:-0.4190
## Median : 0.002531 Median : 0.2476 Median : 0.5110 Median : 0.3346
## Mean : 0.000000 Mean : 0.0000 Mean : 0.0000 Mean : 0.0000
## 3rd Qu.: 0.635178 3rd Qu.: 0.9570 3rd Qu.: 0.5110 3rd Qu.: 1.0883
## Max. : 1.267826 Max. : 0.9570 Max. : 1.1482 Max. : 1.0883
## Zuhören Umweltbewusstsein Interesse
## Min. :-2.68836 Min. :-2.6047 Min. :-2.9437
## 1st Qu.:-0.68760 1st Qu.:-0.5980 1st Qu.:-0.8629
## Median :-0.02067 Median : 0.0709 Median : 0.5244
## Mean : 0.00000 Mean : 0.0000 Mean : 0.0000
## 3rd Qu.: 0.64625 3rd Qu.: 0.7398 3rd Qu.: 0.5244
## Max. : 1.31317 Max. : 1.4087 Max. : 1.2180Die Daten wurden richtig skaliert, da der Mittelwert aller Variablen über alle Beobachtungen 0 ist.
4 Zusammenhänge in den Daten
Wir verwenden den Befehl corrplot() für die Erstinspektion von bivariaten Beziehungen zwischen den Variablen. Das Argument order = "hclust" ordnet die Zeilen und Spalten entsprechend der Ähnlichkeit der Variablen in einer hierarchischen Cluster-Lösung der Variablen (mehr dazu im Teil Clusteranalyse) neu an.
library(corrplot)## corrplot 0.92 loadedcorrplot(cor(Werte.sc), order="hclust")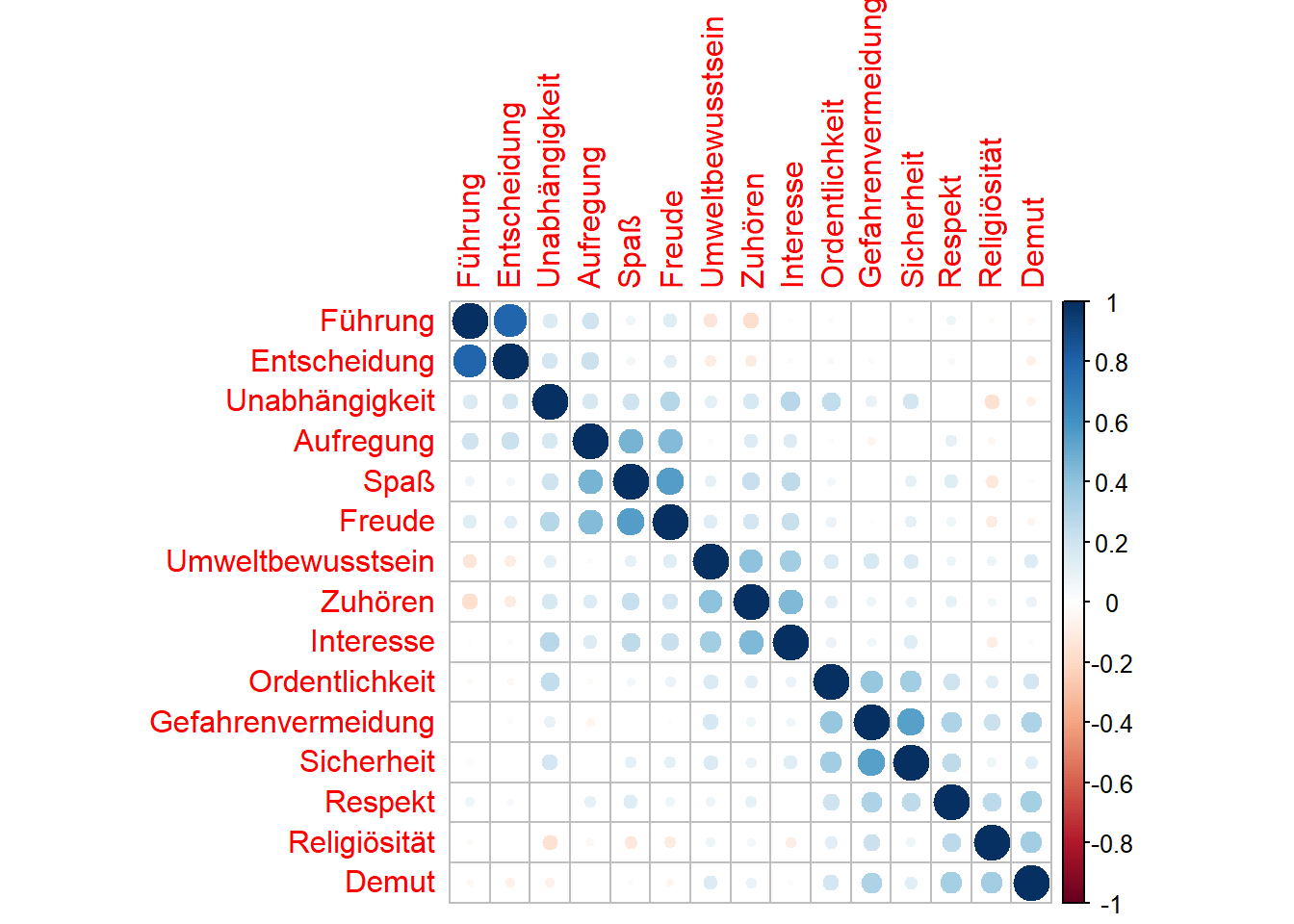
Die Visualisierung der Korrelation der Variablen scheint fünf Cluster zu zeigen:
- (“Führung”, “Entscheidung”)
- (“Aufregung”, “Spaß”, “Freude”)
- (“Umweltbewusstsein”, “Zuhören”, “Interesse”)
- (“Ordentlichkeit”, “Gefahrenvermeidung”, “Sicherheit”)
- (“Respekt”, “Religiösität”, “Demut”)
5 Daten mit fehlende Werten
Wenn in den Daten leere Zellen, also fehlende Werte, vorhanden sind, dann kann es bei bestimmten Rechenoperationen zu Fehlermeldungen kommen. Dies betrifft zum Beispiel Korrelationen, PCA und EFA. Der Ansatz besteht deshalb darin, NA-Werte explizit zu entfernen. Dies kann am einfachsten mit dem Befehl na.omit() geschehen:
Beispiel:
corrplot(cor(na.omit((Werte.sc), order="hclust"))Da wir in unserem Datensatz vollständige Daten verwenden, gibt es auch keine Leerzellen.
Hinweis: In vielen Funktionen gibt es auch die Option na.rm = TRUE, die fehlende Werte entfernt, z. B.:
var(Werte.sc, na.rm = TRUE)6 Hauptkomponentenanalyse (PCA)
Die PCA berechnet ein Variablenset (Komponenten) in Form von linearen Gleichungen, die die linearen Beziehungen in den Daten erfassen. Die erste Komponente erfasst so viel Streuung (Varianz) wie möglich von allen Variablen als eine einzige lineare Funktion. Die zweite Komponente erfasst unkorreliert zur ersten Komponente so viel Streuung wie möglich, die nach der ersten Komponente verbleibt. Das geht so lange weiter, bis es so viele Komponenten gibt wie Variablen.
6.1 Bestimmung der Anzahl der Hauptkomponenten
Betrachten wir in einem ersten Schritt die wichtigsten Komponenten für die Werte. Wir finden die Komponenten mit prcomp().
Werte.pc<- prcomp(Werte.sc)
summary(Werte.pc)## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6 PC7
## Standard deviation 1.6907 1.5422 1.3841 1.14283 1.07975 0.88552 0.8298
## Proportion of Variance 0.1906 0.1585 0.1277 0.08707 0.07772 0.05228 0.0459
## Cumulative Proportion 0.1906 0.3491 0.4768 0.56391 0.64163 0.69391 0.7398
## PC8 PC9 PC10 PC11 PC12 PC13 PC14
## Standard deviation 0.80784 0.78821 0.7599 0.74135 0.68836 0.64775 0.64487
## Proportion of Variance 0.04351 0.04142 0.0385 0.03664 0.03159 0.02797 0.02772
## Cumulative Proportion 0.78332 0.82474 0.8632 0.89988 0.93147 0.95944 0.98716
## PC15
## Standard deviation 0.43884
## Proportion of Variance 0.01284
## Cumulative Proportion 1.00000# Berechnung der Gesamtvarianz
Gesamtvarianz <- sum(Werte.pc$sdev^2)
# Bei sum(Werte.pc$sdev^2) wird die Summe aller 15 Standardabweichungen berechnet.
# Varianzanteil der ersten Hauptkomponente
Werte.pc$sdev[1]^2/Gesamtvarianz## [1] 0.19056896.2 Scree-Plot
Der Standard-Plot plot() für die PCA ist ein Scree-Plot, Dieser zeigt uns in Reihenfolge der Hauptkomponenten jeweils die durch diese Hauptkomponente erfasste Streuung (Varianz). Wir plotten ein Liniendiagramm mit dem Argument type = "l" (l für Linie):
plot(Werte.pc, type="l")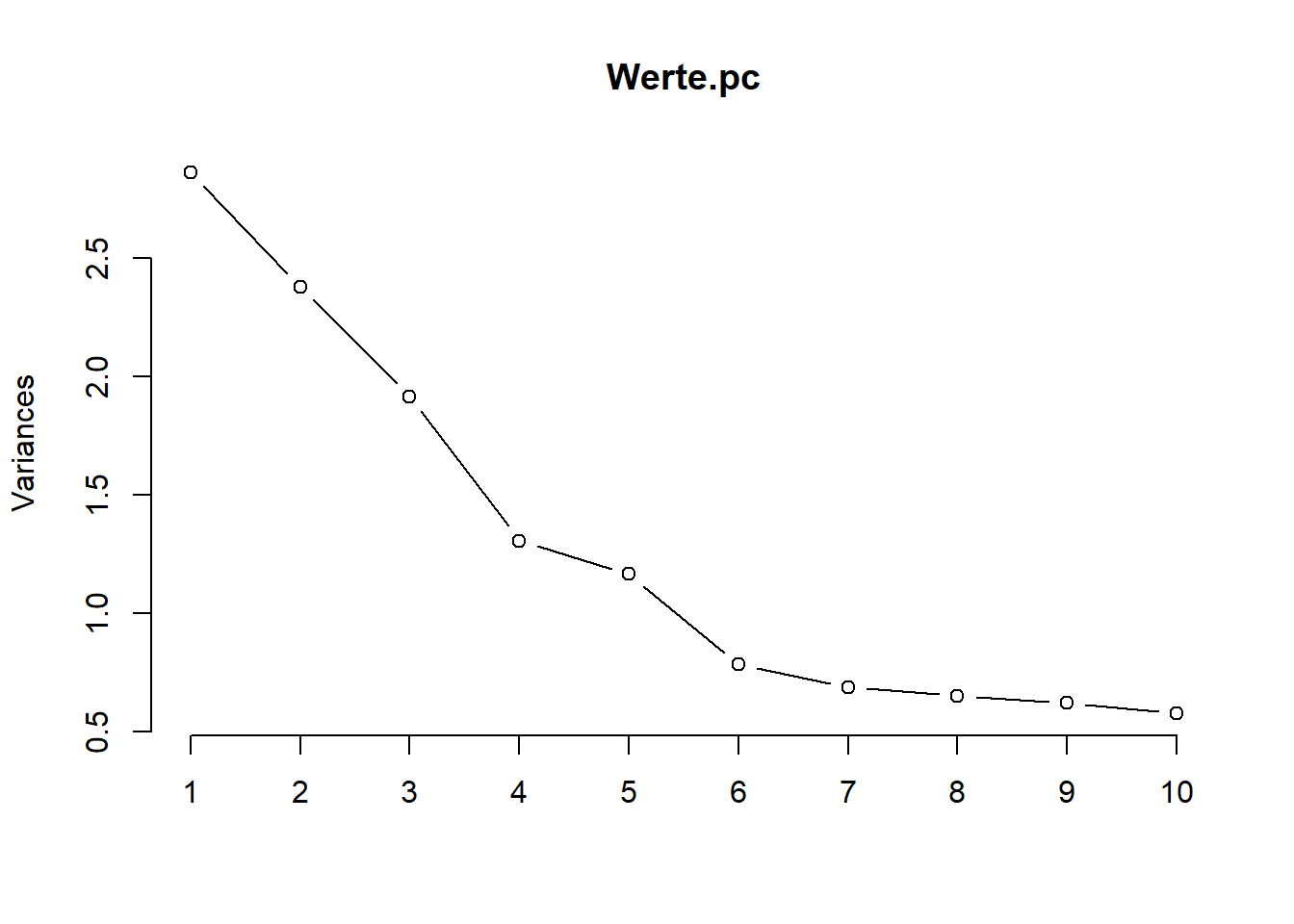
Wir sehen anhand des Scree-Plots, dass bei den Werte-Daten der Anteil der Streuung nach der fünften Komponente nicht mehr wesentlich abnimmt. Es soll die Stelle gefunden werden, ab der die Varianzen der Hauptkomponenten deutlich kleiner sind. Je kleiner die Varianzen, desto weniger Streuung erklärt diese Hauptkomponente.
6.3 Elbow-Kriterium
Nach diesem Kriterium werden alle Hauptkomponenten berücksichtigt, die links von der Knickstelle im Scree-Plot liegen. Gibt es mehrere Knicks, dann werden jene Hauptkomponenten ausgewählt, die links vom rechtesten Knick liegen. Gibt es keinen Knick, dann hilft der Scree-Plot nicht weiter. Bei den Werte-Daten tritt der Ellbogen, je nach Betrachtungsweise, entweder bei vier oder sechs Komponenten auf. Dies deutet darauf hin, dass die ersten fünf Komponenten die meiste Streuung in den Werte-Daten erklären.
6.4 Eigenwert-Kriterium
Der Eigenwert ist eine Metrik für den Anteil der erklärten Varianz. Die Anzahl Eigenwerte können wir über den Befehl eigen() ausgeben.
eigen(cor(Werte))## eigen() decomposition
## $values
## [1] 2.8585328 2.3782591 1.9157861 1.3060498 1.1658554 0.7841482 0.6885614
## [8] 0.6525990 0.6212712 0.5774799 0.5495986 0.4738398 0.4195816 0.4158557
## [15] 0.1925814
##
## $vectors
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] -0.33604416 -0.25622090 -0.128161949 -0.25708630 -0.31686659 -0.08891916
## [2,] -0.33938849 -0.28521782 -0.081849344 -0.15917643 -0.27168790 0.07516516
## [3,] -0.26388043 -0.31660619 0.020871466 -0.35409613 -0.16300892 0.01525403
## [4,] -0.08232717 -0.33393447 0.511129387 0.06869099 0.27375878 -0.08815771
## [5,] -0.08708864 -0.34714315 0.474128588 0.07565331 0.34831269 -0.04338889
## [6,] -0.05342944 0.30307543 0.218554329 -0.38300203 0.21851873 0.29935020
## [7,] -0.23623640 0.21437522 0.256385690 -0.31711196 -0.08949205 -0.11693492
## [8,] -0.15397729 0.32691967 0.171467677 -0.34482751 0.14055059 0.14106740
## [9,] -0.27464246 0.33825802 0.234044155 0.19355770 -0.14567446 -0.26810114
## [10,] -0.30435792 0.21717193 0.166429441 0.32257765 -0.24460149 -0.43448121
## [11,] -0.27346924 0.23434490 0.116388405 0.27914986 -0.16754023 0.54633532
## [12,] -0.29540078 -0.17177961 -0.006053197 0.40251719 -0.00239680 0.49131083
## [13,] -0.31100983 0.05553932 -0.338064762 -0.08652082 0.35043217 0.02771788
## [14,] -0.27757710 0.14689404 -0.248735075 0.03424423 0.39595561 -0.16611769
## [15,] -0.31880702 -0.07337078 -0.274358131 0.12830750 0.37245140 -0.15648663
## [,7] [,8] [,9] [,10] [,11] [,12]
## [1,] 0.01202132 0.041248709 -0.01408612 0.130206897 0.31009355 -0.02696768
## [2,] 0.26627419 0.135852146 -0.08580310 -0.157042163 0.38217601 -0.24114988
## [3,] 0.10078342 0.003367682 0.15291415 0.074930194 -0.73005040 0.30268343
## [4,] 0.01520430 0.055026932 -0.07919406 0.108873884 0.07015185 -0.07370359
## [5,] 0.05838507 -0.038565529 -0.06111274 0.096609791 0.02274680 -0.09446330
## [6,] 0.46059789 -0.328175909 0.38723990 -0.195176261 0.19617221 0.12114616
## [7,] -0.53964197 -0.422986131 -0.37907293 -0.148699391 0.10393977 0.19427884
## [8,] -0.28547974 0.709911656 0.08261177 -0.024519209 -0.04440720 -0.17554504
## [9,] 0.13054104 0.123139927 0.16569043 -0.004325198 -0.11465862 -0.16313432
## [10,] 0.11076199 -0.115161722 0.20479717 -0.084083249 -0.06376440 -0.03363296
## [11,] 0.10897837 -0.020664210 -0.24850940 0.584651315 0.01333556 0.17246152
## [12,] -0.25152458 -0.024186081 0.11560439 -0.599990338 -0.11045917 -0.02350423
## [13,] -0.11763325 -0.352104105 0.05618006 0.237563841 -0.20176120 -0.64134659
## [14,] 0.39099628 0.156832775 -0.58303462 -0.256953030 -0.10337042 0.21220308
## [15,] -0.24316239 0.081935458 0.41348810 0.198545304 0.29517385 0.48735507
## [,13] [,14] [,15]
## [1,] 0.676083103 0.239639453 -0.014012424
## [2,] -0.556270220 -0.237090974 -0.026889620
## [3,] -0.103662222 -0.052357923 0.016105582
## [4,] 0.007483174 0.050894991 0.706143396
## [5,] 0.050783912 0.009339351 -0.698648864
## [6,] 0.074648018 0.069167377 0.045368717
## [7,] -0.107839123 -0.117816660 -0.016220508
## [8,] -0.064457279 0.220164114 -0.056024044
## [9,] 0.283295448 -0.667112771 0.008995238
## [10,] -0.240797718 0.583661212 -0.038214621
## [11,] -0.061627837 0.051558150 -0.004438732
## [12,] 0.167934268 0.027612969 0.029341249
## [13,] -0.026203185 0.030445815 0.061558203
## [14,] 0.101912203 0.063464930 0.019925600
## [15,] -0.132005347 -0.140461650 -0.002008972Der Eigenwert einer Komponente/ eines Faktors sagt aus, wie viel Varianz dieser Faktor an der Gesamtvarianz aufklärt. Laut dem Eigenwert-Kriterium sollen nur Faktoren mit einem Eigenwert größer 1 extrahiert werden. Dies sind bei den Werte-Daten fünf Komponenten/ Faktoren, da fünf Eigenwerte größer 1 sind. Der Grund ist, dass Komponenten/ Faktoren mit einem Eigenwert kleiner als 1 weniger Erklärungswert haben als die ursprünglichen Variablen.
Dies kann auch grafisch mit dem VSS.Scree geplotet werden.
library(psych)
VSS.scree(Werte)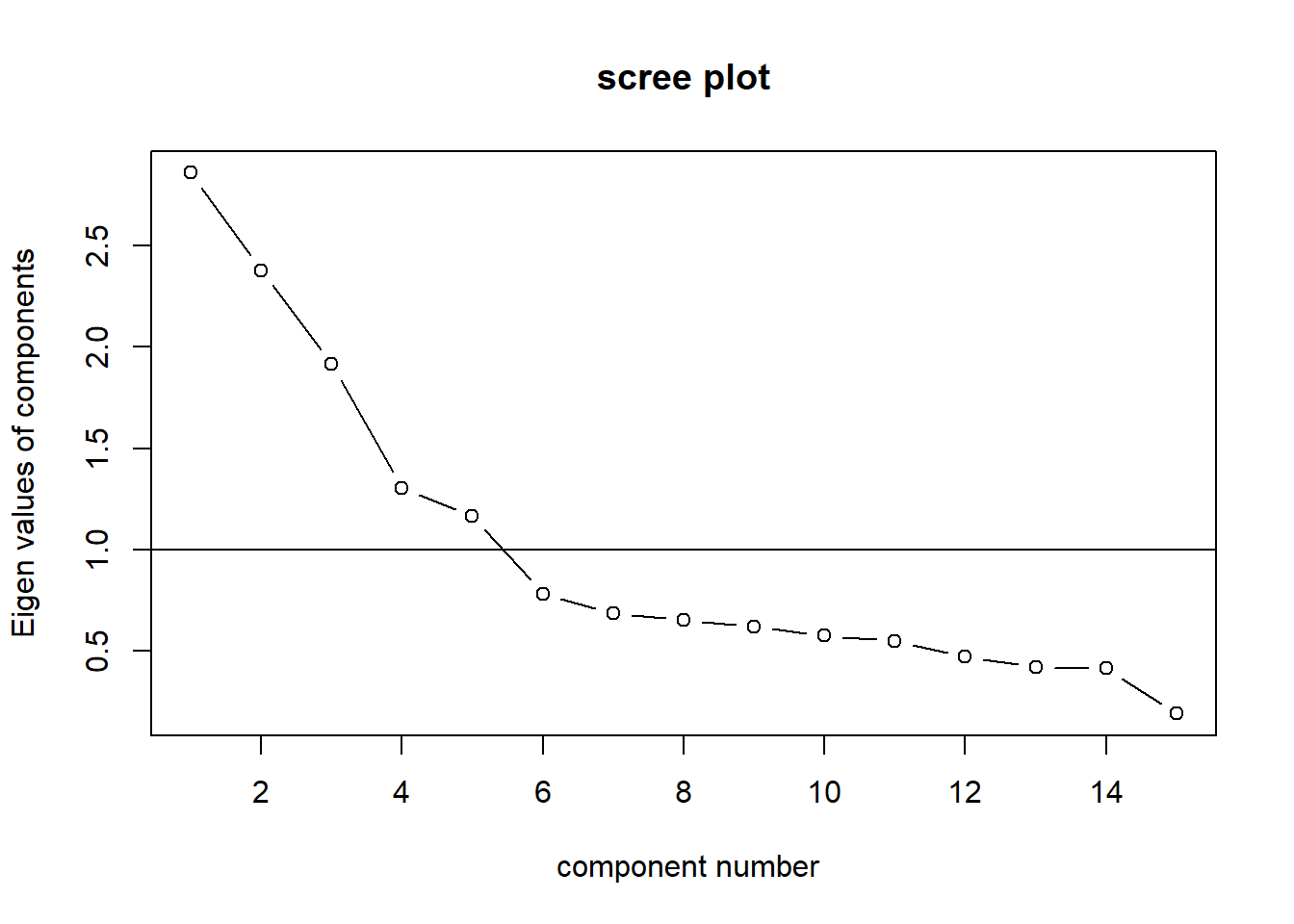
6.5 Biplot
Eine gute Möglichkeit die Ergebnisse der PCA zu analysieren, besteht darin, die ersten Komponenten zuzuordnen, die es uns ermöglichen, die Daten in einem niedrigdimensionalen Raum zu visualisieren. Eine gemeinsame Visualisierung ist ein Biplot. Dies ist ein zweidimensionales Diagramm von Datenpunkten in Bezug auf die ersten beiden Hauptkomponenten, die mit einer Projektion der Variablen auf die Komponenten überlagert wird.
Dazu verwenden wir biplot():
biplot(Werte.pc)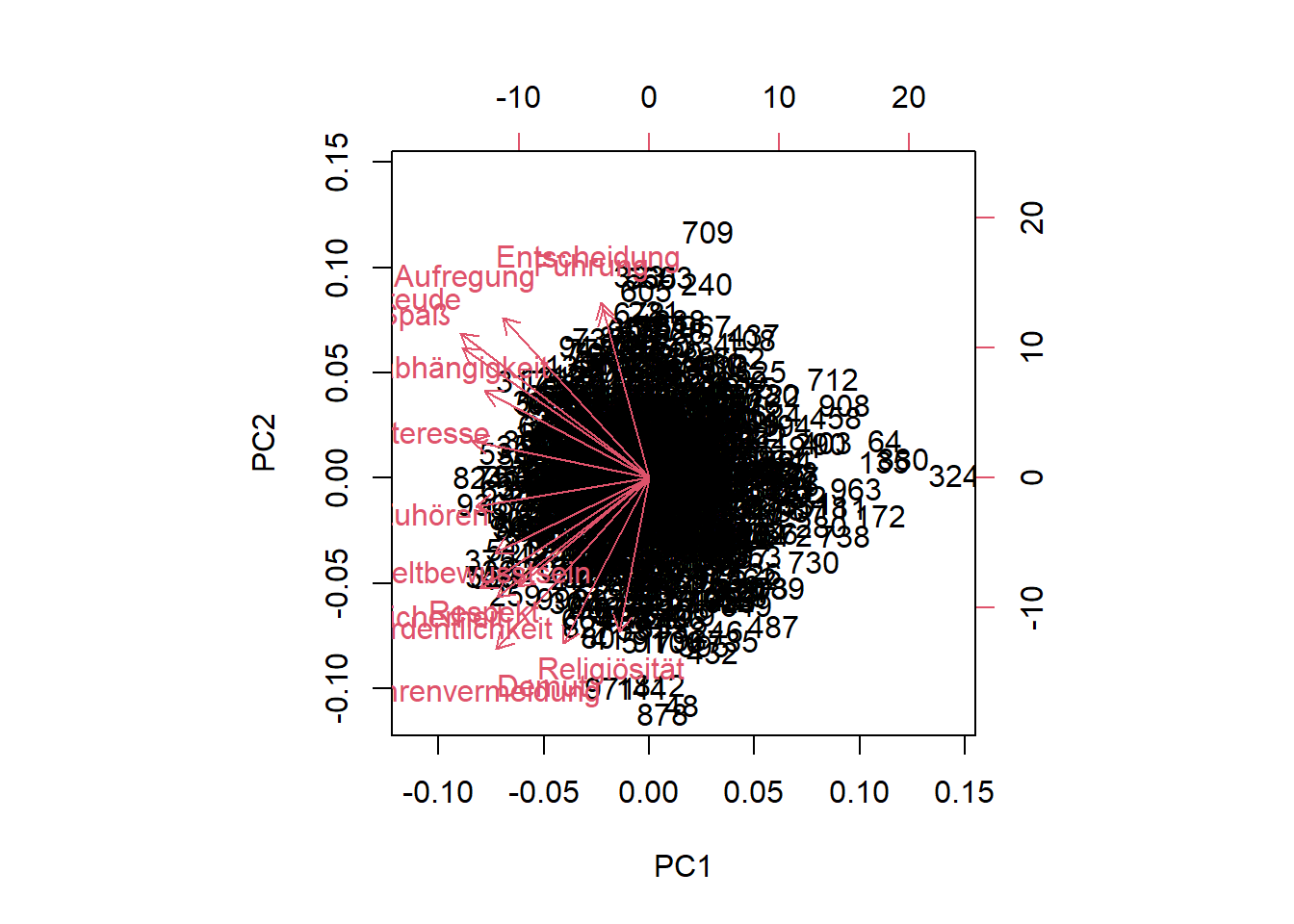
Die Variablen-Gruppierungen sind als rote Ladungspfeile sichtbar. Zusätzlich erhalten wir einen Einblick in die Bewertungscluster (als dichte Bereiche von Beobachtungspunkten). Der Biplot ist hier durch die große Anzahl an Beobachtung recht unübersichtlich.
Am einfachsten lassen sich die Komponenten extrahieren mit dem principal-Befehl aus dem psych-Paket (ist durch das Paket nFactors bereits geladen)
Werte.pca<-principal(Werte, nfactors=5)
print(Werte.pca, cut=0.4, sort = TRUE, digits=2)## Principal Components Analysis
## Call: principal(r = Werte, nfactors = 5)
## Standardized loadings (pattern matrix) based upon correlation matrix
## item RC1 RC2 RC3 RC5 RC4 h2 u2 com
## Spaß 1 0.83 0.71 0.29 1.1
## Freude 2 0.78 0.65 0.35 1.2
## Aufregung 3 0.76 0.63 0.37 1.2
## Sicherheit 10 0.79 0.64 0.36 1.0
## Gefahrenvermeidung 9 0.75 0.67 0.33 1.3
## Ordentlichkeit 11 0.70 0.50 0.50 1.1
## Unabhängigkeit 12 0.42 0.53 0.47 4.2
## Entscheidung 5 0.94 0.89 0.11 1.0
## Führung 4 0.92 0.88 0.12 1.1
## Zuhören 13 0.77 0.66 0.34 1.2
## Interesse 15 0.76 0.63 0.37 1.2
## Umweltbewusstsein 14 0.73 0.57 0.43 1.2
## Religiösität 6 0.74 0.57 0.43 1.1
## Demut 8 0.72 0.56 0.44 1.2
## Respekt 7 0.62 0.54 0.46 1.8
##
## RC1 RC2 RC3 RC5 RC4
## SS loadings 2.08 2.02 1.89 1.87 1.76
## Proportion Var 0.14 0.13 0.13 0.12 0.12
## Cumulative Var 0.14 0.27 0.40 0.52 0.64
## Proportion Explained 0.22 0.21 0.20 0.19 0.18
## Cumulative Proportion 0.22 0.43 0.62 0.82 1.00
##
## Mean item complexity = 1.4
## Test of the hypothesis that 5 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0.07
## with the empirical chi square 1037.66 with prob < 1.6e-191
##
## Fit based upon off diagonal values = 0.886.6 Interpretation der Ergebnisse der PCA
- Das Ergebnis sieht sehr gut aus. Es laden immer mehrere Items (mindestens 2) hoch (> 0,5) auf einer Komponente (die mit RC1 bis RC5 bezeichnet werden, RC steht für Rotated Component). Innerhalb einer PCA kann die Interpretierbarkeit über eine Rotation erhöht werden. Wenn die Rotation nicht ausgeschlossen wird (mit dem Argument
rotate="none"), dann ist die Voreinstellung eineVarimax-Rotation.
- Es gibt keine Items die auf mehr als einer Komponente hoch laden. Die Ladungen sind Korrelationskoeffizienten zwischen den Items und den Hauptkomponenten. * In der Zeile SS loadings finden wir die Eigenwerte der fünf Hauptkomponenten. Den Anteil an der Gesamtvarianz, den sie erklären, findet man in der Zeile Proportion Var. Aufsummiert sind die Anteile in der Zeile Cumlative Var. Insgesamt werden durch die fünf Hauptkomponenten 64% der Gesamtvarianz erklärt.
- Einzig das Item W15 lädt auf keine der Hauptkomponenten hoch.
Um die inhaltliche Bedeutung der Komponenten zu interpretieren, schauen wir uns die Inhalte der jeweiligen Items an und versuchen hierfür einen inhaltlichen Gesamtbegriff zu finden. Die Erste Komponenten könnte mit Genuss, die zweite mit Sicherheit, die dritte mit Bewusstsein, die vierte mit Konformismus und die fünfte mit Anerkennung bezeichnet werden.
| Item | Inhalt des Items |
|---|---|
| Spaß: | Spaß haben und Dinge tun, die Freude bereiten. |
| Freude: | Freuden des Lebens genießen und sich selbst verwöhnen. |
| Aufregung: | Überraschungen mögen und aufregendes Leben führen. |
| Sicherheit: | Im sicheren Umfeld leben und Gefahren meiden. |
| Gefahrenvermeidung: | Interne und externe Sicherheit im Land. |
| Ordentlichkeit: | Wertschätzen von Ordentlichkeit, Sauberkeit und ablehnen von Unordnung. |
| Zuhören: | Andersartigen Menschen zuhören und Meinung verstehen. |
| Umweltbewusstsein: | Für die Natur einsetzen und um die Umwelt kümmern. |
| Interesse: | Interessieren, neugierig sein und versuchen Dinge verstehen. |
| Religiösität: | Religiös sein und auch danach leben. |
| Respekt: | Eltern und ältere Menschen respektieren und gehorsam sein. |
| Demut: | Demütig und bescheiden sein, keine Aufmerksamkeit anziehen. |
| Führung: | Führung übernehmen. |
| Entscheidung: | Entscheidungen treffen. |
Mit der Fubnktion fa.diagram kann das Ergebnis auch grafisch dargestellt werden.
fa.diagram(Werte.pca)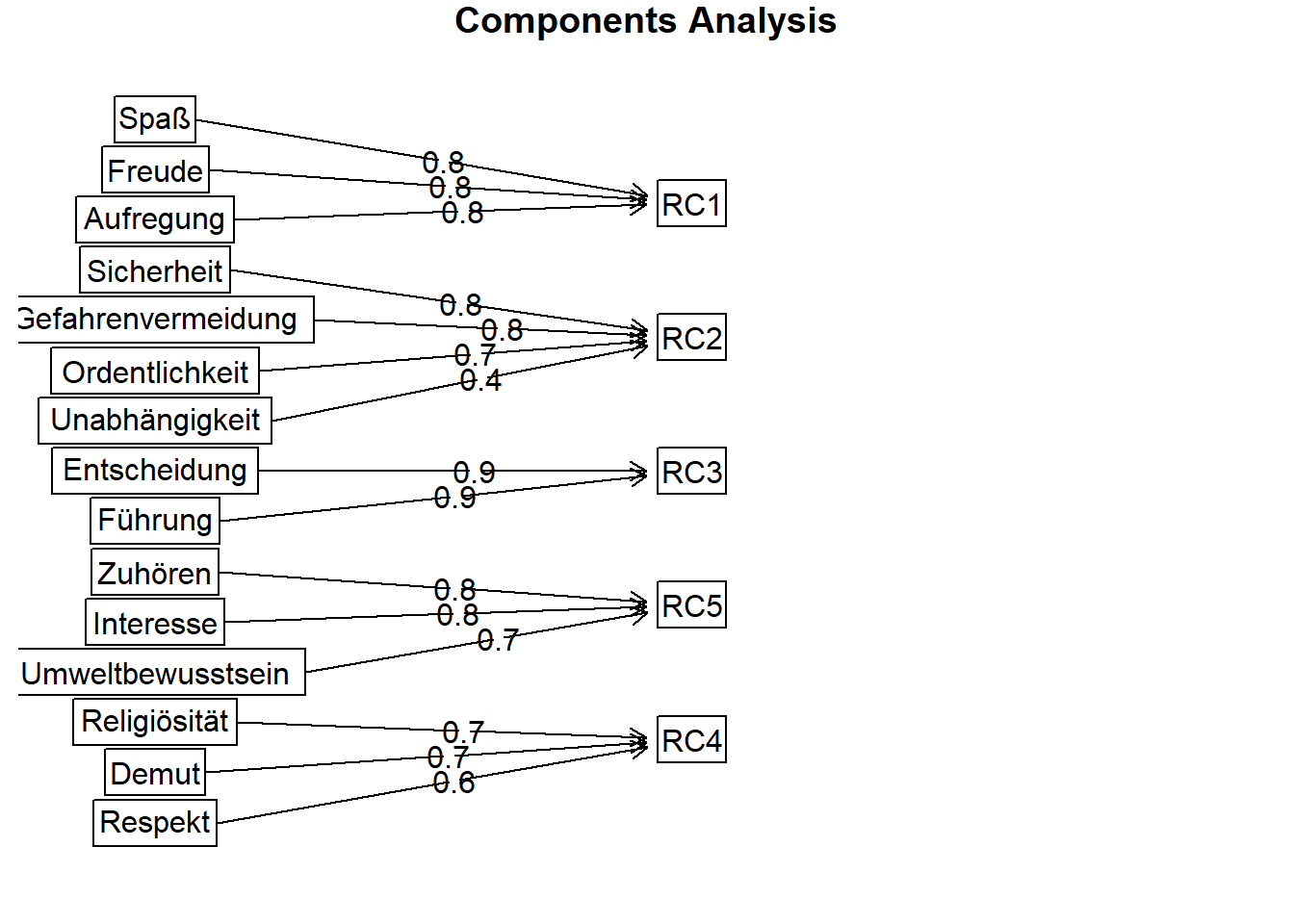
7 Exploratorische Faktorenanalyse (EFA)
EFA ist eine Methode, um die Beziehung von Konstrukten (Konzepten), d. h. Faktoren zu Variablen zu beurteilen. Dabei werden die Faktoren als latente Variablen betrachtet, die nicht direkt beobachtet werden können. Stattdessen werden sie empirisch durch mehrere Variablen beobachtet, von denen jede ein Indikator der zugrundeliegenden Faktoren ist. Diese beobachteten Werte werden als manifeste Variablen bezeichnet und umfassen Indikatoren. Die EFA versucht den Grad zu bestimmen, in dem Faktoren die beobachtete Streuung der manifesten Variablen berücksichtigen.
Das Ergebnis der EFA ist ähnlich zur PCA: eine Matrix von Faktoren (ähnlich zu den PCA-Komponenten) und ihre Beziehung zu den ursprünglichen Variablen (Ladung der Faktoren auf die Variablen). Im Gegensatz zur PCA versucht die EFA, Lösungen zu finden, die in den manifesten variablen maximal interpretierbar sind. Im Allgemeinen versucht sie, Lösungen zu finden, bei denen eine kleine Anzahl von Ladungen für jeden Faktor sehr hoch ist, während andere Ladungen für diesen Faktor gering sind. Wenn dies möglich ist, kann dieser Faktor mit diesem Variablen-Set interpretiert werden.
7.1 Finden einer EFA Lösung
Als erstes muss die Anzahl der zu schätzenden Faktoren bestimmt werden. Hierzu verwenden wir wieder das Ellbow-Kriterium und das Eigenwert-Kriterium. Beide Kriterien haben wir schon bei der PCA verwendet, dabei kommen wir auf 5 Faktoren.
Durch das Paket nFactors bekommen wir eine formalisierte Berechnung der Scree-Plot Lösung mit dem Befehl nScree()
library(nFactors)## Warning: Paket 'nFactors' wurde unter R Version 4.4.1 erstellt## Lade nötiges Paket: lattice##
## Attache Paket: 'nFactors'## Das folgende Objekt ist maskiert 'package:lattice':
##
## parallelnScree(Werte)## noc naf nparallel nkaiser
## 1 5 3 5 5nScree gibt vier methodische Schätzungen für die Anzahl an Faktoren durch den Scree-Plot aus. Wir sehen, dass drei von vier Methoden fünf Faktoren vorschlagen.
7.2 Schätzung der EFA
Eine EFA wird geschätzt mit dem Befehl factanal(x,factors=k), wobei k die Anzahl Faktoren angibt.
Werte.fa<-factanal(Werte, factors=5)
Werte.fa##
## Call:
## factanal(x = Werte, factors = 5)
##
## Uniquenesses:
## Spaß Freude Aufregung Führung
## 0.401 0.486 0.584 0.243
## Entscheidung Religiösität Respekt Demut
## 0.139 0.660 0.662 0.626
## Gefahrenvermeidung Sicherheit Ordentlichkeit Unabhängigkeit
## 0.395 0.481 0.729 0.713
## Zuhören Umweltbewusstsein Interesse
## 0.463 0.666 0.561
##
## Loadings:
## Factor1 Factor2 Factor3 Factor4 Factor5
## Spaß 0.756 0.147
## Freude 0.686 0.149
## Aufregung 0.172 0.611
## Führung 0.849 0.131 -0.133
## Entscheidung 0.921
## Religiösität -0.123 0.568
## Respekt 0.154 0.266 0.492
## Demut 0.168 0.580
## Gefahrenvermeidung 0.715 0.298
## Sicherheit 0.710
## Ordentlichkeit 0.483 0.132 0.137
## Unabhängigkeit 0.188 0.230 0.268 0.265 -0.240
## Zuhören -0.114 0.158 0.698 0.106
## Umweltbewusstsein 0.149 0.539 0.111
## Interesse 0.181 0.618 -0.109
##
## Factor1 Factor2 Factor3 Factor4 Factor5
## SS loadings 1.668 1.600 1.473 1.332 1.116
## Proportion Var 0.111 0.107 0.098 0.089 0.074
## Cumulative Var 0.111 0.218 0.316 0.405 0.479
##
## Test of the hypothesis that 5 factors are sufficient.
## The chi square statistic is 93.28 on 40 degrees of freedom.
## The p-value is 3.83e-06Eine übersichtlichere Ausgabe bekommen wir mit dem print Befehl, in dem wir zusätzlich noch die Dezimalstellen kürzen mit digits=2, alle Ladungen kleiner als 0,5 ausblenden mit cutoff=.4 und die Ladungen mit sort=TRUE so sortieren, dass die Ladungen, die auf einen Faktor laden, untereinander stehen.
print(Werte.fa, digits=2, cutoff=.4, sort=TRUE)##
## Call:
## factanal(x = Werte, factors = 5)
##
## Uniquenesses:
## Spaß Freude Aufregung Führung
## 0.40 0.49 0.58 0.24
## Entscheidung Religiösität Respekt Demut
## 0.14 0.66 0.66 0.63
## Gefahrenvermeidung Sicherheit Ordentlichkeit Unabhängigkeit
## 0.39 0.48 0.73 0.71
## Zuhören Umweltbewusstsein Interesse
## 0.46 0.67 0.56
##
## Loadings:
## Factor1 Factor2 Factor3 Factor4 Factor5
## Führung 0.85
## Entscheidung 0.92
## Spaß 0.76
## Freude 0.69
## Aufregung 0.61
## Gefahrenvermeidung 0.72
## Sicherheit 0.71
## Zuhören 0.70
## Umweltbewusstsein 0.54
## Interesse 0.62
## Religiösität 0.57
## Demut 0.58
## Respekt 0.49
## Ordentlichkeit 0.48
## Unabhängigkeit
##
## Factor1 Factor2 Factor3 Factor4 Factor5
## SS loadings 1.67 1.60 1.47 1.33 1.12
## Proportion Var 0.11 0.11 0.10 0.09 0.07
## Cumulative Var 0.11 0.22 0.32 0.40 0.48
##
## Test of the hypothesis that 5 factors are sufficient.
## The chi square statistic is 93.28 on 40 degrees of freedom.
## The p-value is 3.83e-06Standardmäßig wird bei factanal() eine Varimax-Rotation durchgeführt (das Koordinatensystem der Faktoren wird so rotiert, das eine optimale Zuordnung zu den Variablen erfolgt). Bei Varimax gibt es keine Korrelationen zwischen den Faktoren. Sollen Korrelationen zwischen den Faktoren zugelassen werden, empfiehlt sich die Oblimin-Rotation mit dem Argument rotation="oblimin" aus dem Paket GPArotation.
7.3 Heatmap mit Ladungen
In der obigen Ausgabe werden die Item-to-Faktor-Ladungen angezeigt. Im zurückgegebenen Objekt Werte.fa sind diese als $loadings vorhanden. Wir können die Item-Faktor-Beziehungen mit einer Heatmap von $loadings visualisieren:
library (gplots)## Warning: Paket 'gplots' wurde unter R Version 4.4.1 erstellt##
## Attache Paket: 'gplots'## Das folgende Objekt ist maskiert 'package:stats':
##
## lowessheatmap.2(Werte.fa$loadings)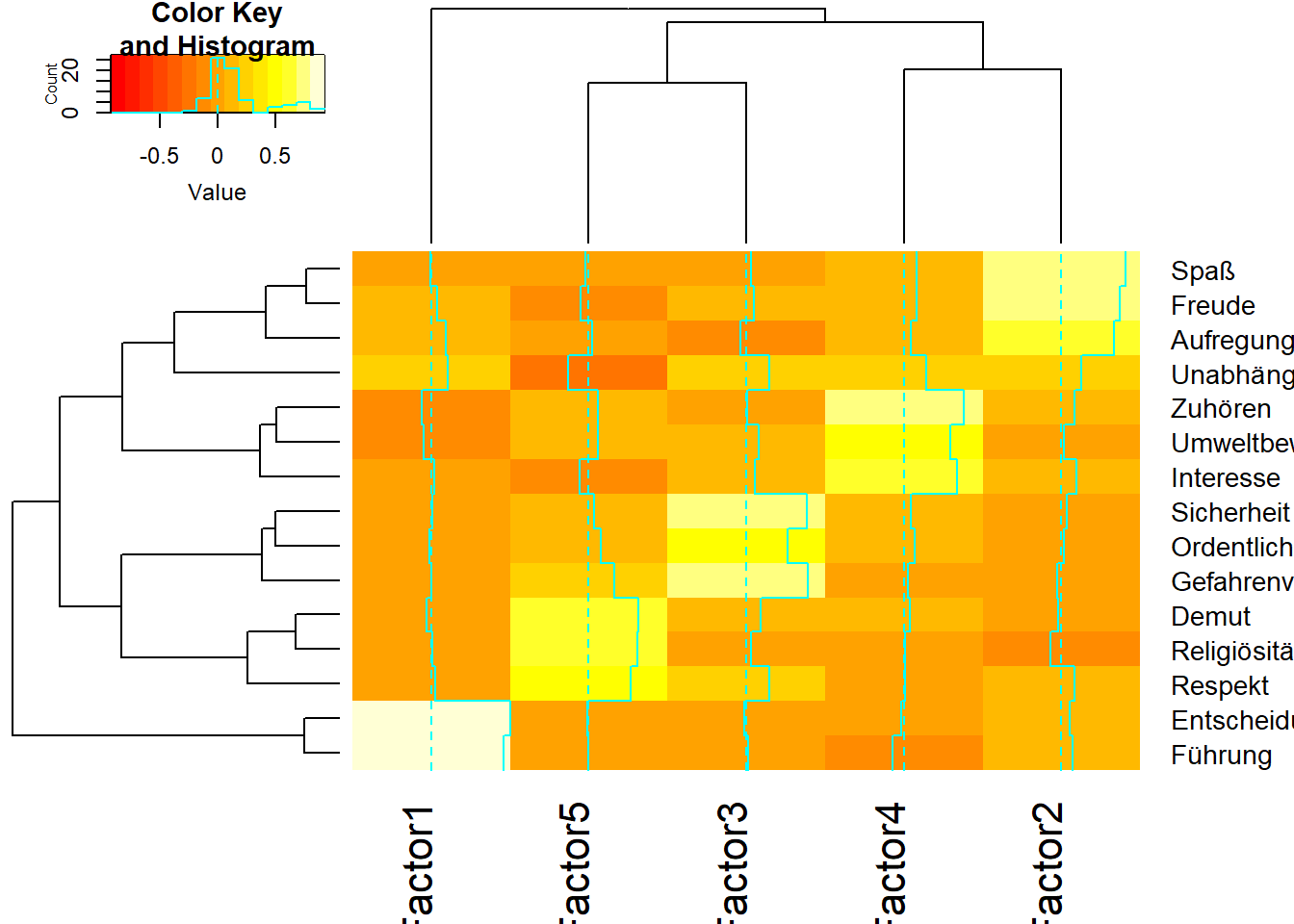
Das Ergebnis aus der Heatmap zeigt eine deutliche Trennung der Items in 5 Faktoren, die interpretierbar sind als Anerkennung, Genuss, Sicherheit, Bewusstsein und Konformismus.
7.4 Berechnung der Faktor-Scores
Zusätzlich zur Schätzung der Faktorstruktur kann die EFA auch die latenten Faktorwerte für jede Beobachtung schätzen. Die gängige Extraktionsmethode ist die Bartlett-Methode.
Werte.ob <- factanal(Werte, factors=5, scores="Bartlett")
Werte.scores <- data.frame(Werte.ob$scores)
names(Werte.scores) <- c("Anerkennung", "Genuss", "Sicherheit", "Bewusstsein", "Konformismus")
head(Werte.scores)## Anerkennung Genuss Sicherheit Bewusstsein Konformismus
## 1 1.3800613 0.9847458 0.5632629 0.1731918 -0.1062450
## 2 -1.4035495 -0.7210411 1.5965857 1.1664029 0.6950300
## 3 1.5320158 -0.6574901 1.6721041 -2.0027410 0.2390436
## 4 -0.5790217 2.3443732 -1.0564093 -1.1195018 -0.1176405
## 5 0.2344081 -1.6524010 1.1888042 -1.7013443 0.4374048
## 6 -0.1303264 0.1110535 -1.0532476 0.7911486 -1.0034994Wir haben nun anstatt der 15 Variablen 5 Faktoren mit Scores. Die Dimensionen wurden um ein Drittel reduziert.
7.5 Interne Konsistenz der Skalen
Das einfachste Maß für die interne Konsistenz ist die Split-Half-Reliabilität. Die Items werden in zwei Hälften unterteilt und die resultierenden Scores sollten in ihren Kenngrößen ähnlich sein. Hohe Korrelationen zwischen den Hälften deuten auf eine hohe interne Konsistenz hin. Das Problem ist, dass die Ergebnisse davon abhängen, wie die Items aufgeteilt werden. Ein üblicher Ansatz zur Lösung dieses Problems besteht darin, den Koeffizienten Alpha (Cronbachs Alpha) zu verwenden.
Der Koeffizient Alpha ist der Mittelwert aller möglichen Split-Half-Koeffizienten, die sich aus verschiedenen Arten der Aufteilung der Items ergeben. Dieser Koeffizient variiert von 0 bis 1. Formal ist es ein korrigierter durchschnittlicher Korrelationskoeffizient.
Faustregeln für die Bewertung von Cronbachs Alpha:
| Alpha | Bedeutung |
|---|---|
| größer 0,9 | exzellent |
| größer 0,8 | gut |
| größer 0,7 | akzeptabel |
| größer 0,6 | fragwürdig |
| größer 0,5 | schlecht |
Wir bewerten nun die interne Konsistent der Items Beispielhaft für das Konstrukt Sicherheit und nehmen zur Demonstration das Item W15 mit in die Analyse auf.
alpha(Werte[, c("Gefahrenvermeidung", "Sicherheit","Ordentlichkeit", "Unabhängigkeit")], check.keys=TRUE)##
## Reliability analysis
## Call: alpha(x = Werte[, c("Gefahrenvermeidung", "Sicherheit", "Ordentlichkeit",
## "Unabhängigkeit")], check.keys = TRUE)
##
## raw_alpha std.alpha G6(smc) average_r S/N ase mean sd median_r
## 0.64 0.63 0.6 0.3 1.7 0.018 5.4 1 0.29
##
## 95% confidence boundaries
## lower alpha upper
## Feldt 0.6 0.64 0.67
## Duhachek 0.6 0.64 0.67
##
## Reliability if an item is dropped:
## raw_alpha std.alpha G6(smc) average_r S/N alpha se var.r
## Gefahrenvermeidung 0.51 0.51 0.42 0.26 1.05 0.026 0.0058
## Sicherheit 0.50 0.49 0.42 0.24 0.97 0.027 0.0203
## Ordentlichkeit 0.54 0.53 0.49 0.28 1.15 0.025 0.0543
## Unabhängigkeit 0.68 0.69 0.61 0.42 2.19 0.017 0.0110
## med.r
## Gefahrenvermeidung 0.25
## Sicherheit 0.25
## Ordentlichkeit 0.19
## Unabhängigkeit 0.38
##
## Item statistics
## n raw.r std.r r.cor r.drop mean sd
## Gefahrenvermeidung 1000 0.75 0.73 0.64 0.49 5.0 1.6
## Sicherheit 1000 0.75 0.75 0.65 0.52 5.7 1.4
## Ordentlichkeit 1000 0.73 0.72 0.55 0.45 5.2 1.6
## Unabhängigkeit 1000 0.52 0.56 0.29 0.23 5.6 1.3
##
## Non missing response frequency for each item
## 1 2 3 4 5 6 7 miss
## Gefahrenvermeidung 0.02 0.06 0.12 0.15 0.21 0.25 0.19 0
## Sicherheit 0.01 0.03 0.05 0.11 0.18 0.27 0.35 0
## Ordentlichkeit 0.02 0.05 0.10 0.14 0.19 0.25 0.25 0
## Unabhängigkeit 0.01 0.02 0.06 0.11 0.22 0.31 0.28 0Bei dem Konstrukt Sicherheit können wir durch Elimination von Unabhängigkeit das Cronbachs Alpha von 0,64 auf einen fast akzeptablen Wert von 0,68 erhöhen.
Das Argument check.keys=TRUE gibt uns eine Warnung aus, sollte die Ladung eines oder mehrerer Items negativ sein. Dies ist hier nicht der Fall, somit müssen auch keine Items recodiert werden.
8 Literatur
- Chris Chapman, Elea McDonnell Feit (2015): R for Marketing Research and Analytics, Kapitel 8.1-8.3
- Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani (2013): An Introduction to Statistical Learning – with Applications in R, http://www-bcf.usc.edu/~gareth/ISL/, Kapitel 10.2, 10.4
- Reinhold Hatzinger, Kurt Hornik, Herbert Nagel (2011): R – Einführung durch angewandte Statistik. Kapitel 11
- Maike Luhmann (2015): R für Einsteiger, Kapitel 19