1.1 Definition des Forschungsproblems

Ein Problem bezieht sich auf die allgemeinen Fragen, für die das Unternehmen Antworten benötigt. Es sind drei Fragen zu beantworten.

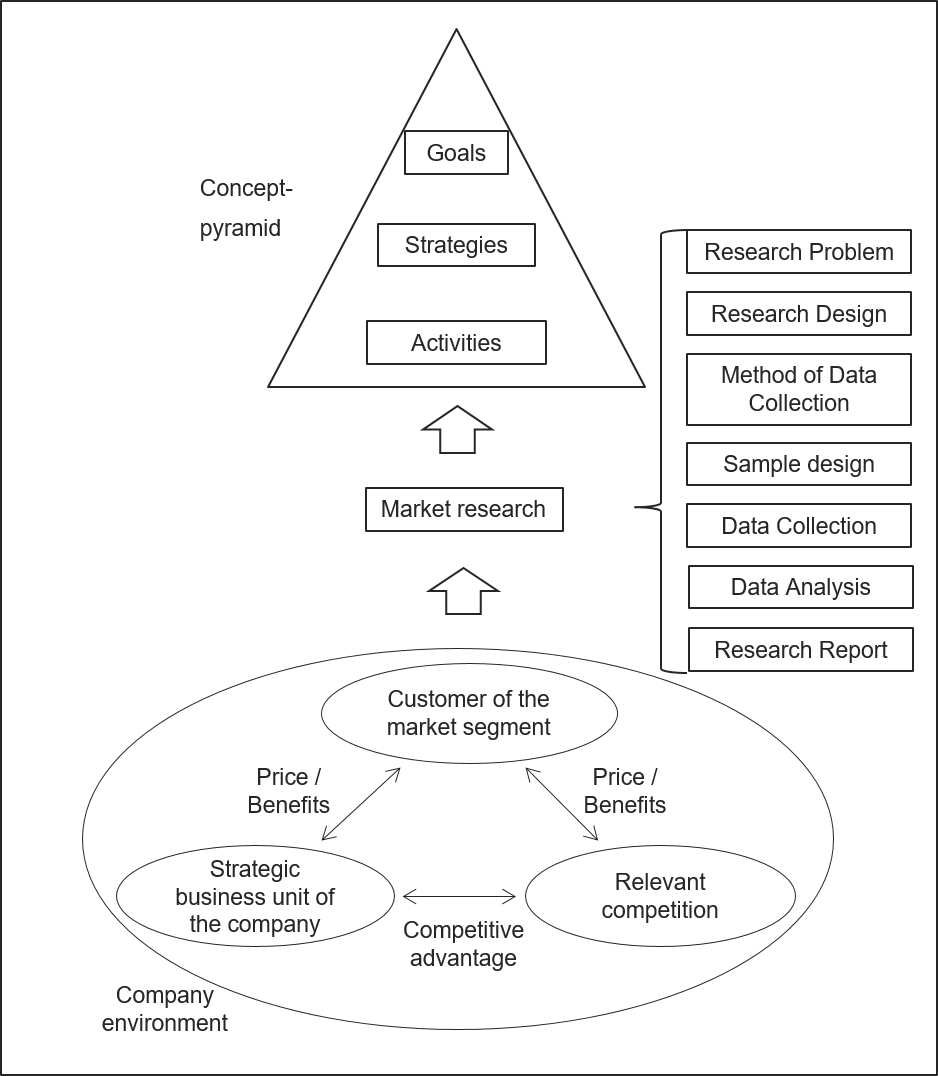
• Was ist das Forschungsziel und welche Fragen soll die Forschung beantworten? Das strategische Dreieck kann zur Analyse der Situation verwendet werden, wenn das Problem nicht direkt aus dem Unternehmen ersichtlich ist. Es könnte zum Beispiel klar sein, dass die Umsätze des Unternehmens rückläufig sind. Die Stärken-Schwächen-Analyse und die Deckungsbeitragsanalyse zeigen z.B., dass das Vertriebsprogramm des Unternehmens veraltet ist. Diese Phase endet in der Regel mit dem Bedarf an weiteren Informationen (durch Marktforschung), um ein neues Konzept mit den inhaltlichen Zielen, Strategien und Maßnahmen zu erstellen. Das Bindeglied zwischen dem strategischen Dreieck (Abbildung 1) und der Konzeptpyramide besteht aus Informationen zu den drei Eckpunkten des strategischen Dreiecks und der Analyse und Weiterleitung der relevanten Informationen für die Erstellung eines neuen Unternehmenskonzepts (Gansser 2014a).

• Was ist die interessierende Grundgesamtheit und wie ist diese beschaffen? Bei unzureichender Definition der Grundgesamtheit, systematisch verzerrter Auswahl der Auskunftspersonen oder schlampiger Umsetzung der Selektionskriterien können die Ergebnisse der Untersuchung erheblich von den Verhältnissen in der interessierenden Grundgesamtheit abweichen. Dies gilt es zu vermeiden.

• Welche internen und externen Faktoren beeinflussen die aktuelle Situation? Die Analyse der exogenen Einflüsse führt zu einer Analyse des Umfelds. In diesem Zusammenhang werden die Chancen und Risiken aus dem allgemeinen Umfeld (Umfeldanalyse), den relevanten Märkten, den Absatzmärkten, den Beschaffungsmärkten, dem Kapitalmarkt und dem Arbeitsmarkt (Marktanalyse) und dem relevanten Wirtschaftszweig insgesamt betrachtet. Interne Faktoren als Ursache für eine Krise beschränken sich in der Regel auf die Betrachtung der strategischen Geschäftseinheit eines Unternehmens. Dabei wird der leistungserstellende Bereich auch durch den Bereich des Unternehmensmanagements beeinflusst (Gansser 2014a).

Abb. 1: Die Rolle der Marktforschung im Zusammenspiel mit Unternehmenskonzept und Situationsanalyse

1.2 Definition des Forschungsdesigns

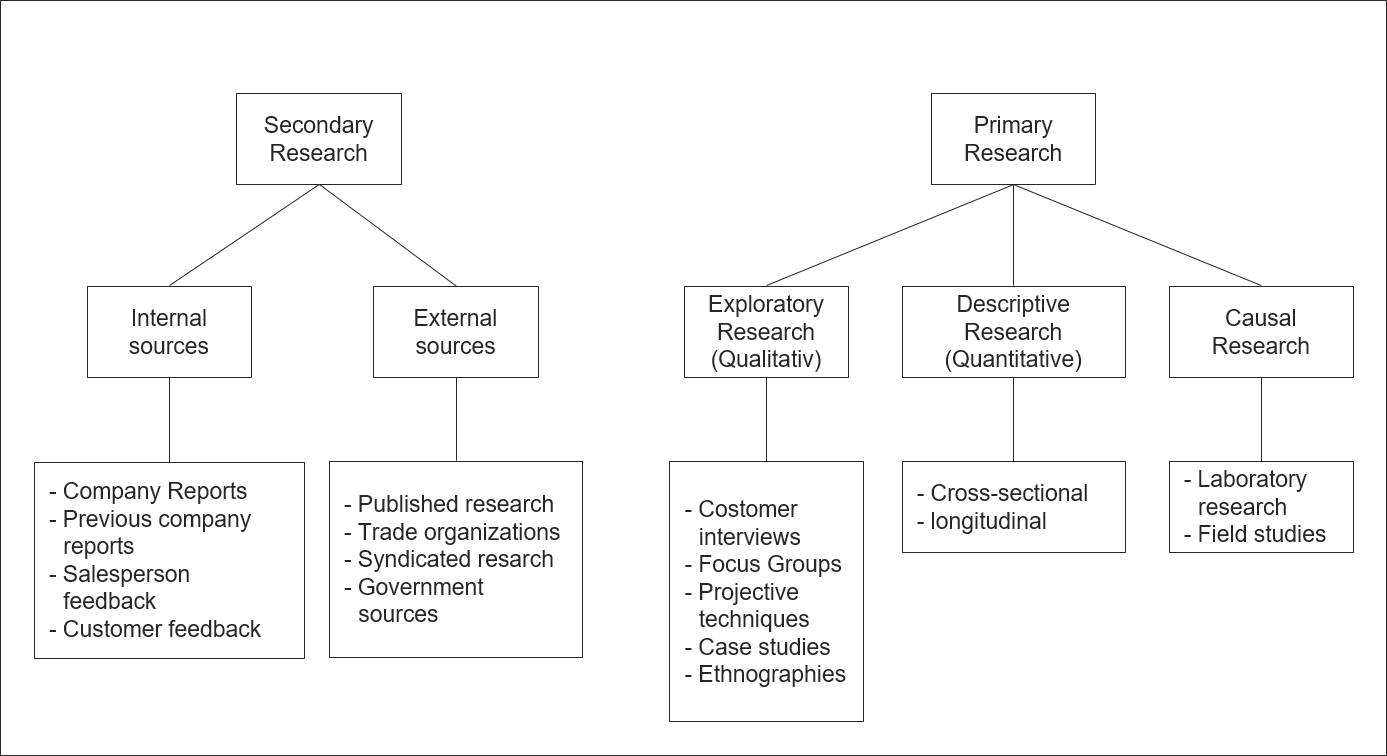
Das Forschungsdesign konkretisiert, welche Informationen Vermarkter sammeln und welche Art von Studie sie durchführen. Forschungsdesigns fallen in zwei Kategorien: Sekundärforschung und Primärforschung. Nicht alle Forschungsprobleme benötigen die gleichen Forschungstechniken, und Marketer lösen viele Probleme am effektivsten mit einer Kombination verschiedener Techniken. In einem ersten Schritt müssen Marktforscher immer fragen, ob die Informationen, die sie für ihre Entscheidung benötigen, bereits vorhanden sind. Daten, die für einen anderen als den spezifischen Zweck bestimmt sind, werden als Sekundärdaten bezeichnet. Informationen, die für eine bestimmte Fragestellung beschafft werden, nennt man Primärdaten. Zu den Primärdaten gehören demografische und psychologische Informationen über Kunden und Interessenten, Einstellungen und Meinungen der Kunden zu Produkten und Konkurrenzprodukten sowie ihre Bekanntheit oder ihr Wissen über ein Produkt und ihre Überzeugungen über die Menschen, die diese Produkte verwenden.

Abb. 2: Forschungsdesigns (basierend auf Solomon et al. 2017)

1.3 Methode zur Datenerhebung von Primärdaten

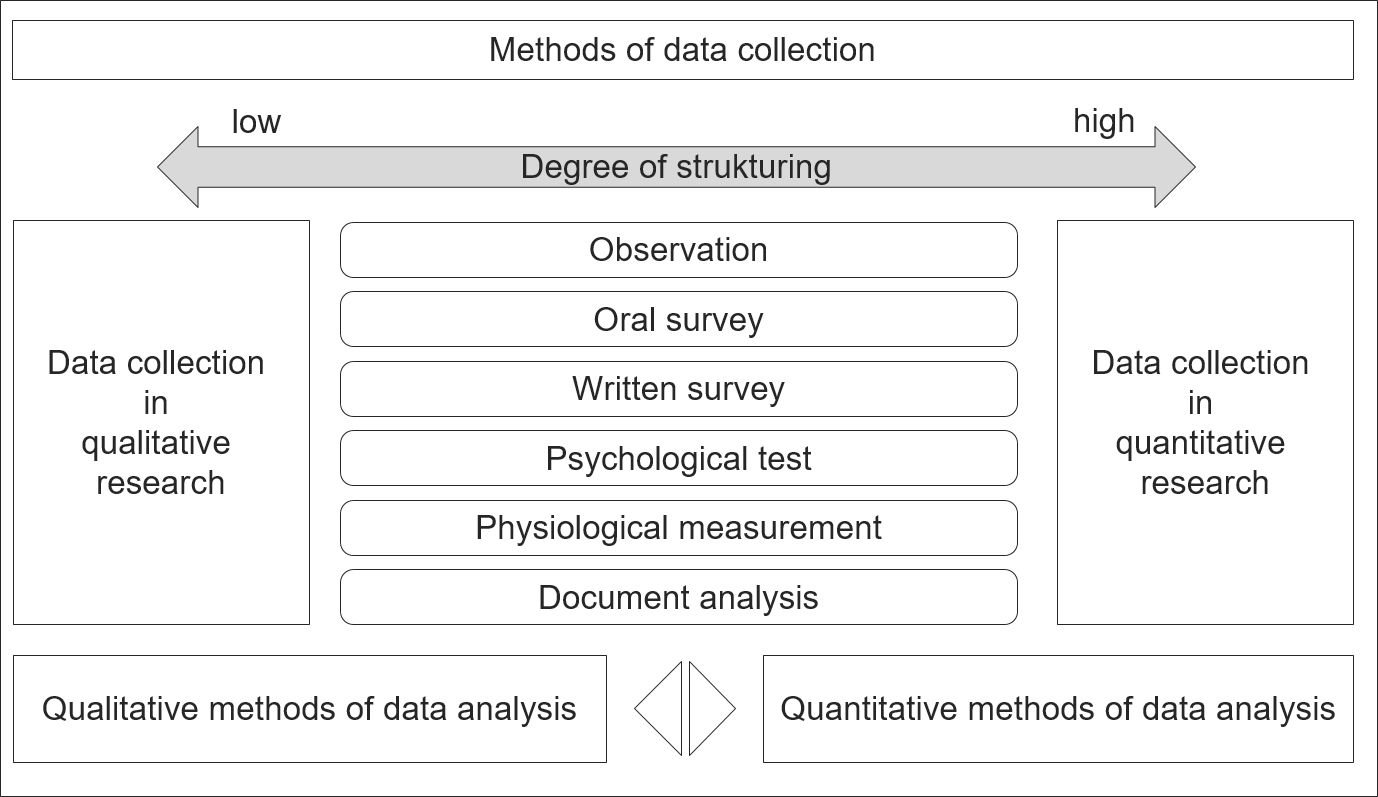
Methoden der Primärdatenerhebung werden entweder als Befragung oder als Beobachtung beschrieben. Der Grad der Strukturierung ist bei quantitativen Datenerhebungsmethoden sehr hoch. Qualitative Datenerhebungsmethoden sind nicht oder nur teilweise strukturiert. Es ist zu betonen, dass die Datenerhebungsinstrumente für qualitative und quantitative Forschung gleich sind. Abbildung 3 verdeutlicht dies. Charakteristischerweise beeinflussen drei Faktoren die Qualität von Forschungsergebnissen: Validität, Zuverlässigkeit und Repräsentativität. Validität ist das Ausmaß, in dem die Forschung das misst, was sie messen soll. Reliabilität ist das Ausmaß, in dem die Messverfahren der Forschung frei von Fehlern sind. Repräsentativität ist das Ausmaß, in dem die Verbraucher in einer Studie einer größeren Gruppe gleichen, an der die Organisation ein Interesse hat. Es geht um die Vorhersagbarkeit der Möglichkeit, dass alle Elemente der Grundgesamtheit in die Stichprobe fallen.

Abb. 3: Qualitative versus quantitative Forschung

1.4 Design der Stichprobe

Marktforscher erheben in der Regel die meisten ihrer Daten aus einer Stichprobe der interessierenden Population. Anhand der Antworten aus dieser Stichprobe schließen sie auf die Grundgesamtheit. Ob solche Rückschlüsse zutreffend oder ungenau sind, hängt von der Art und Qualität der Stichprobe ab. Es gibt zwei Haupttypen von Stichproben: Wahrscheinlichkeitsstichproben und Nicht-Wahrscheinlichkeitsstichproben. Eine Wahrscheinlichkeitsstichprobe ist eine Wahrscheinlichkeitsstichprobe ist eine Stichprobe, in der jedes Mitglied der Grundgesamtheit eine bekannte Chance hat, enthalten zu sein. enthalten ist. Eine Nicht-Wahrscheinlichkeitsstichprobe ist eine Stichprobe, bei der die Befragten nach persönlichem Ermessen ausgewählt werden, und eine Zufallsstichprobe ist eine Nicht-Wahrscheinlichkeitsstichprobe, die aus Personen besteht, die zufällig verfügbar sind, wenn und wo die Daten erhoben werden.

1.5 Datenerfassung

Primärdaten können auf viele Arten erhoben werden. Umfragen, physische Messungen und Beobachtung sind drei der Möglichkeiten. Die Qualität unserer Schlussfolgerungen ist nur so gut, wie die Daten sind. Die gleiche Logik gilt für die Personen, die die Daten sammeln: Die Qualität der Forschungsergebnisse ist nur so gut wie der schlechteste Interviewer in der Studie. Deshalb müssen die Interviewer geschult und betreut werden.

1.6 Datenanalyse und Dateninterpretation

Die Grundvoraussetzung für die Datenanalyse ist die Bestimmung des Messniveaus der vorliegenden Daten. Die Anwendung besonders leistungsfähiger Methoden der Statistik ist in der Regel nur dann zulässig, wenn bestimmte Messniveaus vorhanden sind. Messen ist die Zuordnung von Zahlen oder anderen Symbolen zu Merkmalen von Objekten nach bestimmten, vorgegebenen Regeln. Skalierung ist die Erzeugung eines Kontinuums, auf dem sich die gemessenen Objekte befinden. Es gibt vier primäre Messskalen: nominale, ordinale und metrische (Intervall und Verhältnis). Eine Nominalskala ist eine Skala, deren Zahlen nur als Etiketten oder Markierungen zur Identifizierung und Klassifizierung von Objekten dienen, wobei eine strikte Eins-zu-eins-Entsprechung zwischen den Zahlen und den Objekten besteht. Eine Ordinalskala ist eine Rangskala, bei der den Objekten Zahlen zugewiesen werden, um das relative Ausmaß anzugeben, in dem ein bestimmtes Merkmal vorhanden ist. So lässt sich feststellen, ob ein Objekt mehr oder weniger von einem Merkmal besitzt als ein anderes Objekt. Intervallskala ist eine Skala, bei der die Zahlen verwendet werden, um Objekte so zu ordnen, dass numerisch gleiche Abstände auf der Skala gleiche Abstände in dem zu messenden Merkmal darstellen. Die Verhältnisskala ist die höchste Skala. Diese Skala ermöglicht es dem Forscher, Objekte zu identifizieren oder zu klassifizieren, die Objekte in eine Rangfolge zu bringen und Intervalle oder Unterschiede zu vergleichen. Es ist auch sinnvoll, Verhältnisse von Skalenwerten zu berechnen (Malhotra 2009).

Qualität der Daten: Dies bezieht sich darauf, wie normal die Daten verteilt sind. Die ersten besprochenen Techniken sind empfindlich gegenüber den Annahmen der Linearität, Normalität und der gleichen Varianz der Daten. Untersuchungen der Verteilung, der Schiefe und der Neugier sind hilfreich bei der Untersuchung der Verteilung. Es ist auch wichtig, die Größe der fehlenden Werte in den Beobachtungen zu verstehen und zu entscheiden, ob sie ignoriert oder Werte auf die fehlenden Beobachtungen bezogen werden sollen. Ein weiteres Maß für die Datenqualität sind Ausreißer, und es ist wichtig zu bestimmen, ob die Ausreißer wieder verschoben werden sollen. Wenn sie festgehalten werden, können sie eine Verzerrung der Daten verursachen; wenn sie eliminiert werden, können sie bei den Normalitätsannahmen helfen. Der Schlüssel ist, zu versuchen zu verstehen, was die Ausreißer repräsentieren (Diez et al. 2014).

Einteilung der statistischen Methoden:

• Deskriptive Datenanalyse: Eine Aufgabe der statistischen Methoden ist es, Daten über viele Einzelfälle (z. B. Verbraucher, Unternehmen) zusammenzufassen. Dabei werden statistische Messgrößen und Darstellungen in Form von Tabellen und Grafiken verwendet.
• Multivariate analytische Methoden: In der Marktforschung müssen sich Marketer mit komplexen Zusammenhängen zwischen zahlreichen Variablen auseinandersetzen. So lassen sich Aspekte des Konsumentenverhaltens (z.B. Markenwahl, Art der Bedürfnisse) kaum durch eine Variable erklären, und der Erfolg oder Misserfolg eines Produktes hängt nie von einem Faktor (z.B. Werbebudget oder Preis) ab. Für Marketer spielen daher multivariate Analysemethoden, die für die gleichzeitige Analyse vieler Variablen geeignet sind, eine wichtige Rolle (Malhotra 2009).

1. Abhängigkeitsanalysen: Es gibt Verfahren, die darauf abzielen, eine abhängige Variable durch eine bestimmte Anzahl unabhängiger Variablen zu erklären, z. B. den Marktanteil eines Produktes durch Werbebudgets, Preis, Kaufkraft der Zielgruppe, relative Produktqualität etc. Gängige Verfahren sind Varianzanalyse, Regression und Conjoint Measurement
2. Interdependenzanalysen: Bei anderen multivariaten Verfahren stehen Zusammenhänge zwischen einer größeren Anzahl von Variablen im Vordergrund. Die Variablen werden nicht als abhängig oder unabhängig klassifiziert, sondern es wird die Gesamtheit der interdependenten Beziehungen untersucht. Gängige Verfahren sind die Hauptkomponentenanalyse, die explorative Faktorenanalyse und die Clusteranalyse.

1.7 Bericht über die Forschungsergebnisse

Der letzte Schritt in der Marktforschung besteht darin, über die Forschungsergebnisse zu berichten und die Ergebnisse zu dokumentieren. Generell muss ein Forschungsbericht klar und prägnant sein. Die Leser - Top-Management, Kunden, Kreativabteilungen und viele andere - müssen die Forschungsergebnisse leicht verstehen können.

2.1 Varianzanalyse

Mit der Varianzanalyse (ANOVA) kann überprüft werden, ob ein signifikanter Unterschied zwischen zwei oder mehreren Mittelwerten besteht. Die Varianzanalyse eignet sich besonders für den Vergleich zwischen Gruppen, was wiederum ihre Anwendung für die Auswertung von Experimenten erklärt, bei denen Vergleiche zwischen Messwerten aus Versuchs- und Kontrollgruppen vorgenommen werden müssen. Die Anzahl der Gruppen (unabhängige Variable) bestimmt, ob es sich um eine einfaktorielle Analyse (eine Gruppe) oder eine mehrfaktorielle Analyse (mehrere Gruppen) handelt. Bei der Varianzanalyse wird zwischen der erklärten und unerklärten Varianz der abhängigen (metrischen) Variablen unterschieden. Der Einfluss der unabhängigen Variablen (Gruppenzugehörigkeit) wird anhand des Verhältnisses zwischen erklärter und unerklärter Varianz beurteilt. Eine der zentralen Ideen der Varianzanalyse ist es, die Varianzen der abhängigen Variablen innerhalb der Gruppen mit den Varianzen zwischen den Gruppen (Abweichungen der Gruppenmittelwerte vom Gesamtmittelwert) zu vergleichen. Ist die Varianz zwischen den Gruppen groß im Vergleich zur Varianz innerhalb der Gruppen, so deutet dies auf einen deutlichen Einfluss der unabhängigen Variablen hin, der die Gruppenzugehörigkeit bestimmt.

Annahmen der Varianzanalyse (Diez et al. 2014):

• Der Fehlerterm muss normalverteilt sein, was gleichzeitig eine Normalverteilung der Messwerte in der Grundgesamtheit ist.
• Der Fehlerterm muss zwischen den Gruppen gleich oder homogen sein.
• Die Messwerte müssen unabhängig voneinander sein.

2.2 Regression

Die zentrale Idee dieser Methode ist, dass die unterschiedlichen Werte einer abhängigen Variablen (Zielvariable) auf eine andere (unabhängige) Variable (Einflussvariable) zurückgeführt werden sollen. In diesem Sinne wird die abhängige Variable durch die unabhängige oder erklärende Variable erklärt. Die Regressionsanalyse ist eine Methode zur Analyse von assoziativen Zusammenhängen zwischen einer metrischen abhängigen Variablen (Zielvariable) und einer oder mehreren unabhängigen Variablen (Einflussvariable). Sie kann auf folgende Arten verwendet werden: - Um festzustellen, ob die unabhängigen Variablen eine signifikante Variation in der abhängigen Variablen erklären: ob ein Zusammenhang besteht. - Um zu bestimmen, wie viel der Variation in der abhängigen Variablen durch die unabhängigen Variablen erklärt werden kann: Stärke des Zusammenhangs. - Um die Struktur oder Form der Beziehung zu bestimmen: die mathematische Gleichung, die die unabhängigen und abhängigen Variablen miteinander verbindet. - Zur Vorhersage der Werte der abhängigen Variablen. - Zur Kontrolle anderer unabhängiger Variablen bei der Bewertung der Beiträge bestimmter Variablen oder eines Satzes von Variablen.

Schritte der Regressionsanalyse (Diez et al 2014, Chapman und Feit 2015, Malhotra 2009):

1. Formulierung des Regressionsmodells: Basierend auf theoretischen und empirischen Erkenntnissen sowie bisherigen Erfahrungen muss bestimmt werden, welche unabhängigen Variablen die interessierende (abhängige) Variable erklären könnten.
2. Schätzung der Parameter des Regressionsmodells: Für die Schätzung des Regressionsmodells sind einige Annahmen notwendig, die der einschlägigen Literatur entnommen werden können.

Ein Regressionsmodell im bivariaten Fall sieht so aus

Y= b0 + b1*X

und im multiplen (multivariaten) Fall

Y = b0 + b1X1+ b2X2+ bn*Xn

wobei Y = abhängige Variable, X = unabhängige Variable, b0 = Achsenabschnitt und b1-n = Steigung der Variablen

Die am häufigsten verwendete Technik zur Anpassung einer Funktion ist eine minimale quadratische Schätzung (Verfahren der kleinsten Quadrate). Dieses Verfahren ermittelt die beste Anpassung durch Minimierung der vertikalen Abstände aller Beobachtungen. Die ermittelten Parameter (Regressionskoeffizienten) bestimmen den Zusammenhang zwischen der unabhängigen und die abhängigen Variable für den untersuchten Datensatz. Mit Hilfe dieser Parameter und den jeweiligen Variablenwerten der unabhängigen Variablen kann der Wert der abhängigen Variablen für den jeweiligen Fall geschätzt werden.

3. Überprüfung der Modellanpassung: Ein wichtiges Maß für die Beurteilung eines Regressionsmodells ist der Anteil der durch das Modell erklärten Varianz an der Gesamtvarianz. Die Stärke des Zusammenhangs wird gemessen durch das Quadrat des multiplen Korrelationskoeffizienten Korrelationskoeffizienten R2 gemessen, der auch als Bestimmtheitsmaß bezeichnet wird. R2 liegt zwischen 0 und 1. Die Extremwerte 0 und 1 bedeuten, dass ein Modell keine Varianz erklärt oder die abhängige Variable vollständig erklärt wird.

2.3 Logistische Regression

Mit der logistischen Regression können die Einflüsse auf eine abhängige nominalskalierte Variable untersucht werden. Es wird angenommen, dass die abhängige Variable dichotom ist, d.h. sie kann nur zwei Werte annehmen (0 und 1). Mit Hilfe mehrerer unabhängiger Variablen werden die Wahrscheinlichkeiten für die Werte der abhängigen Variablen (ein “Ereignis”) geschätzt. In einer multinomialen logistischen Regression können auch kategoriale abhängige Variablen mit mehr als zwei Ausprägungen analysiert werden. Da kein linearer Zusammenhang getestet wird, werden die Regressionskoeffizienten nicht genau wie bei linearen Regressionen interpretiert. Es kann nur die Richtung des Einflusses interpretiert werden.

2.4 Dimensionsreduktion mit PCA und EFA (Ausführlicher und mit Daten unter Dimensionsreduktion)

Daten haben oft viele Variablen - oder Dimensionen - und es ist von Vorteil, sie auf eine kleinere Anzahl von Variablen (oder Dimensionen) zu reduzieren. Zusammenhänge zwischen Konstrukten können deutlicher identifiziert werden. Es gibt zwei gängige Methoden, um die Komplexität von multivariaten metrischen Daten zu reduzieren, indem die Anzahl der Dimensionen in den Daten verringert wird (Chapmann und Feit 2014): - Die Hauptkomponentenanalyse (PCA) versucht, unkorrelierte Linearkombinationen zu finden, die die maximale Varianz in den Daten erfassen. Die Blickrichtung ist dabei von den Daten zu den Komponenten. - Die explorative Faktorenanalyse (EFA) versucht, die Varianz anhand einer kleinen Anzahl von Dimensionen zu modellieren und gleichzeitig die Dimensionen der ursprünglichen Variablen interpretierbar zu machen. Es wird angenommen, dass die Daten einem Faktorenmodell entsprechen. Die Blickrichtung ist von den Faktoren zu den Daten.

Gründe für die Notwendigkeit der Datenreduktion: - Im technischen Sinne der Dimensionsreduktion können wir anstelle von Variablensätzen die Faktoren-/Komponentenwerte verwenden (z. B. für Mittelwertvergleiche, Regressionsanalysen und Clusteranalysen). - Wir können die Unsicherheit reduzieren. Wenn wir glauben, dass ein Konstrukt nicht eindeutig messbar ist, kann die Unsicherheit mit einem Variablensatz reduziert werden. - Wir können den Aufwand für die Datenerfassung vereinfachen, indem wir uns auf Variablen konzentrieren, von denen bekannt ist, dass sie einen signifikanten Beitrag zum Faktor/zur Komponente von Interesse leisten. Wenn wir feststellen, dass einige Variablen für einen Faktor nicht wichtig sind, können wir sie aus der Aufzeichnung eliminieren.

Hauptkomponentenanalyse(PCA): Die PCA berechnet einen Satz von Variablen (Komponenten) in Form von linearen Gleichungen, die die linearen Beziehungen in den Daten erfassen. Die erste Komponente erfasst so viel Varianz wie möglich aus allen Variablen als eine einzige lineare Funktion. Die zweite Komponente erfasst so viel Varianz wie möglich, die nach der ersten Komponente übrigbleibt, unkorreliert zur ersten Komponente. Dies wird so lange fortgesetzt, wie es so viele Komponenten wie Variablen gibt. Um die Anzahl der Komponenten zu entschlüsseln, wird üblicherweise ein Scree Plot verwendet. Dieser zeigt uns in der Reihenfolge der Hauptkomponenten die Varianz, die durch diese Hauptkomponente erklärt wird. Es soll der Punkt gefunden werden, ab dem die Varianzen der Hauptkomponenten signifikant kleiner sind. Je kleiner die Varianzen sind, desto weniger Varianz erklärt diese Hauptkomponente. Das Ellenbogenkriterium berücksichtigt alle Hauptkomponenten, die links vom Knickpunkt im Screeplot liegen. Wenn es mehrere Knickpunkte gibt, werden die Hauptkomponenten ausgewählt, die links vom ganz rechten Knickpunkt liegen. Wenn es keinen Knick gibt, ist der Scree Plot nicht hilfreich.

Explorative Faktorenanalyse (EFA): Die EFA ist eine Methode, um die Beziehung von Konstrukten (Konzepten, die Faktoren sind) zu Variablen zu beurteilen. Die Faktoren werden als latente Variablen betrachtet, die nicht direkt beobachtet werden können. Stattdessen werden sie empirisch durch mehrere Variablen beobachtet, von denen jede ein Indikator für die zugrunde liegenden Faktoren ist. Diese beobachteten Werte werden als manifeste Variablen bezeichnet und beinhalten Indikatoren. Die EFA versucht zu bestimmen, inwieweit die Faktoren die beobachtete Varianz der manifesten Variablen berücksichtigen. Das Ergebnis der EFA ist ähnlich wie bei der PCA: eine Matrix von Faktoren (ähnlich den PCA-Komponenten) und deren Beziehung zu den ursprünglichen Variablen (Ladung der Faktoren auf die Variablen). Im Gegensatz zur PCA wird bei der EFA versucht, Lösungen zu finden, die in den manifesten Variablen interpretierbar sind. Im Allgemeinen wird versucht, Lösungen zu finden, bei denen eine kleine Anzahl von Ladungen für jeden Faktor sehr hoch ist, während andere Ladungen für diesen Faktor klein sind. Wenn dies möglich ist, kann dieser Faktor mit diesem Variablensatz interpretiert werden. Innerhalb einer PCA kann die Interpretierbarkeit durch eine Rotation (z. B. Varimax) erhöht werden.

Abb. 4: Eigenwerte der 19 Komponenten der menschlichen Werte

Finden einer EFA-Lösung Zunächst muss die Anzahl der zu schätzenden Faktoren bestimmt werden. Wir verwenden zwei gängige Methoden: das Ellbogenkriterium und die Eigenwerte. Der Eigenwert ist eine Metrik für den Anteil der erklärten Varianz. Der Eigenwert eines Faktors gibt an, wie viel Varianz dieser Faktor zur Gesamtvarianz erklärt. Nach dem Eigenwertkriterium sollen nur Faktoren mit einem Eigenwert größer als 1 extrahiert werden. Sie können auch grafisch mit einem Scree Plot dargestellt werden. Ein Knick im Screeplot in Abbildung 4 konnte bei der fünften Hauptkomponente gefunden werden. Der Screeplot zeigt also eine 5-Faktoren-Lösung.

Dann wird die Faktorenanalyse geschätzt, wobei die Anzahl der zu extrahierenden Faktoren angegeben werden muss. Standardmäßig wird bei der EFA eine Varimax-Rotation durchgeführt (das Koordinatensystem der Faktoren wird so gedreht, dass die Variablen den Variablen optimal zugeordnet werden). Bei der Varimax-Rotation gibt es keine Korrelationen zwischen den Faktoren. Wenn Korrelationen zwischen den Faktoren zulässig sind, wird die Oblimin-Rotation empfohlen.

Interne Konsistenz der Skalen, die den Faktor messen

Das einfachste Maß für die interne Konsistenz ist die Split-half-Reliabilität. Die Items werden in zwei Teile geteilt und die resultierenden Scores sollten in ihren Eigenschaften ähnlich sein. Hohe Korrelationen zwischen den Teilen deuten auf eine hohe interne Konsistenz hin. Das Problem ist, dass die Ergebnisse davon abhängen, wie die Items aufgeteilt werden. Ein gängiger Ansatz zur Lösung dieses Problems ist die Verwendung des Alpha-Koeffizienten (Cronbachs Alpha). Der Koeffizient Alpha ist der Durchschnitt aller möglichen Split-Half-Koeffizienten, die sich aus verschiedenen Arten der Verteilung der Items ergeben. Dieser Koeffizient variiert von 0 bis 1. Formal ist er ein korrigierter durchschnittlicher Korrelationskoeffizient. Regeln für die Bewertung von Cronbachs Alpha: < 0,6 ist schlecht, zwischen 0,6 und 0,7 ist fraglich, zwischen 0,7 und 0,8 ist akzeptabel, zwischen 0,8 und 0,9 ist gut und größer als 0,9 ist ausgezeichnet.

2.5 Mehrdimensionale Skalierung (MDS)

Die MDS ist eine Methode, die auch zum Auffinden niedrigdimensionaler Repräsentationen von Daten verwendet werden kann. Anstatt Komponenten oder latente Faktoren zu extrahieren, wie bei der PCA oder EFA, arbeitet die MDS stattdessen mit Distanzen (oder Ähnlichkeiten). Die MDS versucht, eine niedrig-dimensionale Abbildung zu finden, die alle beobachteten Ähnlichkeiten zwischen Objekten am besten bewahrt. Die von der MDS gelieferten Informationen wurden für eine Vielzahl von Marketinganwendungen genutzt (Malhotra 2009): Imagemessung, Marktsegmentierung, Entwicklung neuer Produkte, Bewertung der Werbewirksamkeit, Preisanalyse, Kanalentscheidungen und Konstruktion von Einstellungsskalen.

In einer Studie zur Erforschung von Verhaltenstypen durch die FOM im Jahr 2016 wurden 22.131 Personen auf einer Skala von 1 bis 7 zu ihren Werten und ihrem Kaufverhalten befragt. Mittels PCA wurden 13 Hauptkomponenten gebildet (5 Dimensionen der menschlichen Werte und 8 Dimensionen des Konsumverhaltens):

• Menschliche Werte sind: Genuss, Wertschätzung, Konformismus, Sicherheit und Bewusstsein.
• Das Konsumverhalten sind: Perfektionistisch, Markenbewusst, Neuheitsmode, Stress, Preis, Impulsiv, Verwirrt und Gewohnheitsmäßig.

Um diese 13 Dimensionen in einem zweidimensionalen Raum darzustellen, wurde eine Metrik MDS berechnet. Zur Berechnung der MDS wurden die einzelnen Dimensionen miteinander korreliert (Produkt-Moment-Korrelation). Bei diesem Ansatz werden die Dimensionen als Punkte im mehrdimensionalen Raum dargestellt, so dass die Abstände zwischen den Punkten die Interkorrelationen der Dimensionen darstellen.

Abb. 5: Wahrnehmungsraum mit 13 Dimensionen der menschlichen Werte und des Konsumentenverhaltens

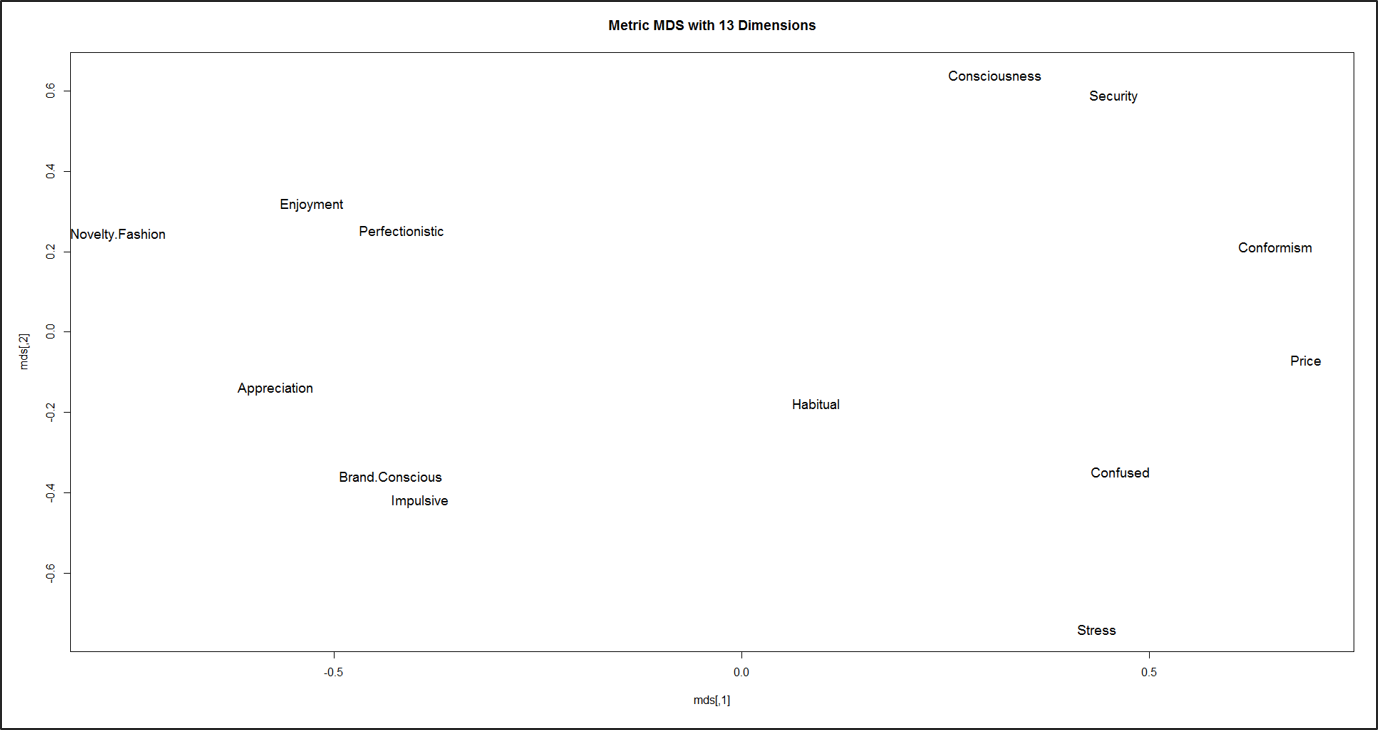
Für nicht-metrische Daten wie Rankings oder kategoriale Variablen wird ein MDS-Algorithmus verwendet, der keine metrischen Distanzen annimmt (Chapman und Feit 2014).
Für die praktische Anwendung ist es wichtig, eine plausible Interpretation des durch die MDS erzeugten Wahrnehmungsraums zu erhalten. In diesem Zusammenhang kann die zusätzliche Integration von unabhängigen Bewertungsdimensionen in den Wahrnehmungsraum mit Hilfe des Vektormodells eine wertvolle Interpretationshilfe darstellen. In einer Vorstudie zu den Verhaltenstypen im Jahr 2014 (n = 15.563) wurden 40 Werte mittels MDS in einem Wahrnehmungsraum berechnet. Zur Interpretation werden nun Merkmalsvektoren in Form der Ausprägungen des Kaufverhaltens in die Konfiguration der MDS-Analyse aufgenommen.

Abb. 6: Wahrnehmungsraum mit einem integrierten Vektormodell (Gansser 2014b)

Methode: - Zunächst wurden die 6 Dimensionen des Kaufverhaltens mit den einzelnen Items der Wertorientierungen korreliert. - Anschließend wurde für jede der Dimensionen des Kaufverhaltens eine lineare Regressionsanalyse durchgeführt. - Die beiden Koordinaten der Werte im MDS sind die unabhängigen Variablen, die zur Erklärung der Varianz des Kaufverhaltens herangezogen werden (hier die Korrelation mit den Werten). - Für das Vektormodell sind die Beta-Koeffizienten der beiden Dimensionen von Interesse. Diese werden als Koordinaten für den zu zeichnenden Vektor verwendet. - Der Vektor verläuft im Diagramm als Gerade durch den Ursprung und den durch diese beiden Koordinaten definierten Punkt, und zwar als Pfeil in Richtung des Punktes.

2.6 Clusteranalyse

Die Clusteranalyse dient dazu, innerhalb der Daten homogene Gruppen (meist Beobachtungen) zu finden, die zwischen den Gruppen möglichst heterogen sind. Eine typische Anwendung der Clusteranalyse ist die Marktsegmentierung oder Kundensegmentierung. Um die Ähnlichkeit von Beobachtungen zu bestimmen, können verschiedene Distanzmaße verwendet werden. Für metrische Merkmale wird z. B. häufig die euklidische Metrik verwendet, d. h. Ähnlichkeit und Abstand werden anhand des euklidischen Abstands bestimmt. Andere Distanzen wie Manhattan oder Gower sind ebenfalls möglich. Diese haben den Vorteil, dass sie nicht nur für metrische Daten, sondern auch für gemischte Variablentypen verwendet werden können.

Typische Schritte einer Clusteranalyse (Chapmann und Feit 2014): - Auswahl der Variablen, die zur Gruppenbildung herangezogen werden sollen (z. B. soziodemografische Merkmale, Einstellungsvariablen, Lebensstilmerkmale). - Quantifizierung von Ähnlichkeiten bzw. Unähnlichkeiten der Objekte anhand eines sogenannten Proximity-Maßes und Ermittlung einer Distanz- bzw. Ähnlichkeitsmatrix. - Zusammenfassung der Objekte zu homogenen Gruppen auf Basis der Werte des Proximitätsmaßes unter Anwendung eines Fusionsalgorithmus.

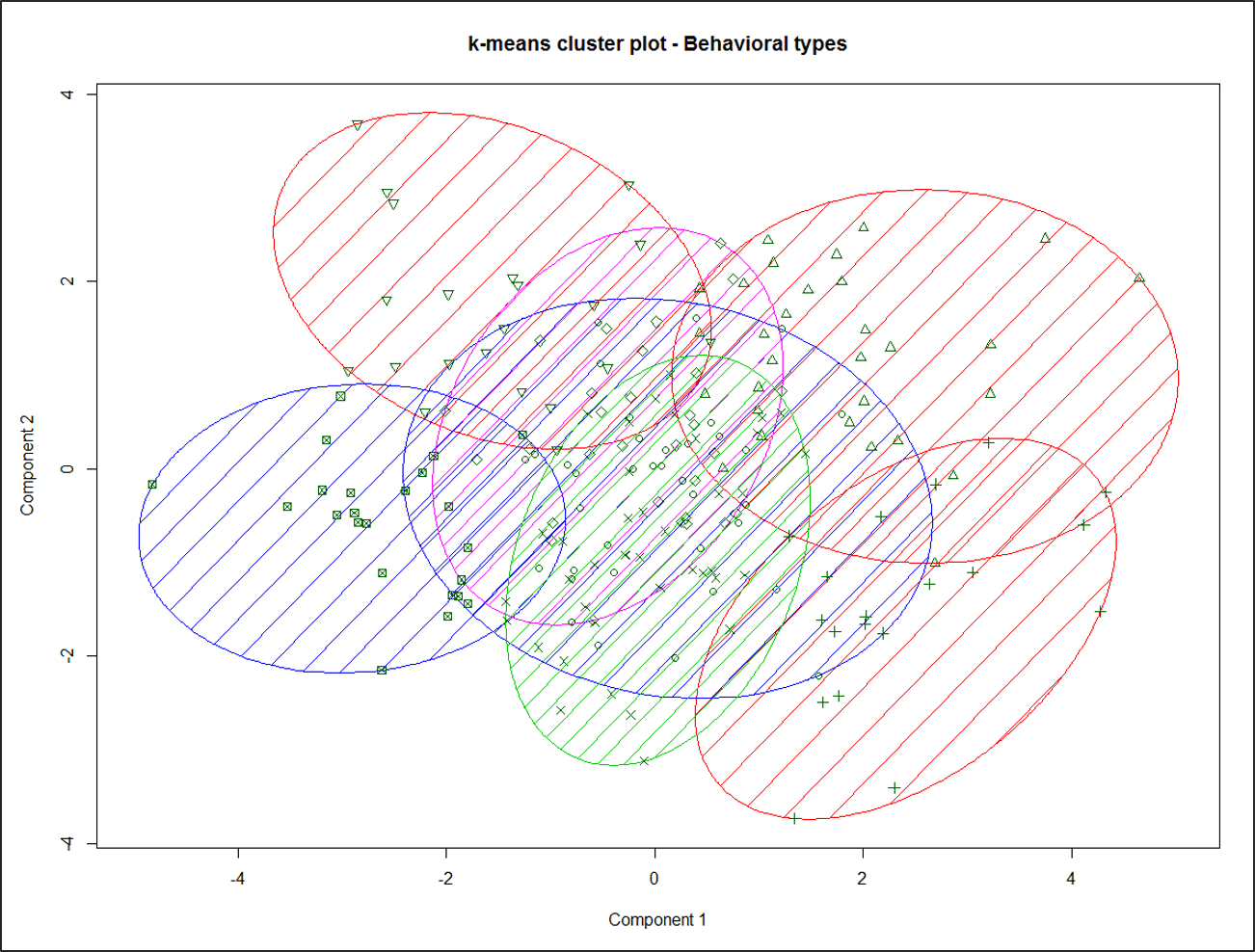
Es gibt zwei Methoden der Clusteranalyse: Hierarchische Verfahren und Partitionierungsverfahren. Bei hierarchischen Clustering-Verfahren werden die Beobachtungen nacheinander zusammengefasst. Zunächst bildet jede Beobachtung ein eigenes Cluster, der dann entsprechend dem Ähnlichkeitsmaß gruppiert wird. Partitionierungsverfahren gehen von einer gegebenen Gruppierung der Objekte aus und ordnen die Objekte zwischen den Gruppen um, bis ein optimaler Wert einer Zielfunktion (die Quadratsumme der Abweichungen der Beobachtungen im Cluster zum Clusterzentrum soll minimiert werden) erreicht ist. Ein typischer Ansatz für die Clusteranalyse ist es, in einem ersten Schritt die Anzahl der Cluster mit hierarchischen Methoden zu bestimmen. Diese Anzahl dient als Voraussetzung für die Anwendung von Partitionierungsverfahren, mit denen in einem zweiten Schritt die Zuordnung der Objekte zu den Clustern zu optimieren versucht wird. In einer Studie der FOM aus dem Jahr 2016 wurden 22131 Personen zu ihren Werten und ihrem Kaufverhalten befragt. Mit Hilfe der PCA wurden 13 Hauptkomponenten gebildet (5 Werte und 8 Kaufverhalten). Eine Clusteranalyse nach dem obigen Verfahren ergab 7 Cluster, die in Abbildung 7 mit einer Stichprobe von n = 200 grafisch dargestellt sind. Der Clusterplot stellt die Clusterzuordnung durch Farbe und Ellipsen gegen die ersten beiden Hauptkomponenten der Prädiktoren dar.

Abb. 7: Clusterplot für die sieben Verhaltenstypen

2.7 Strukturgleichungsmodellierung (SEM)

Strukturgleichungsmodelle sind vor allem in der wissenschaftlichen Forschung weit verbreitet, während die praktische Anwendung dieser Modelle selten, aber nicht unbedeutend ist.

SEM kombinieren die Methoden der Faktorenanalyse und der Regressionsanalyse mit der Möglichkeit, beide Modelle gleichzeitig zu schätzen (Kline 2017). Bei der SEM werden durch Varianzen und Kovarianzen von Indikatoren (manifeste Variablen) Rückschlüsse auf die Abhängigkeiten zwischen Konstrukten (latente Variablen oder Faktoren) gezogen. Der Vorteil ist, dass eine größere Anzahl von interdependenten Abhängigkeiten analysiert werden kann und gleichzeitig latente Variablen in diese Beziehungen einbezogen werden können. Schließlich geht es darum, Theorien zur Existenz von latenten Variablen und deren Zusammenhänge zu untersuchen. Abbildung 8 soll Aspekte der Analyse von multiplen Abhängigkeiten veranschaulichen. Gansser und Krol (2017) untersuchen die Einflussfaktoren auf die Verhaltensabsicht zur Nutzung von Location Based Services. Es fallen sofort die zahlreichen direkten und indirekten Abhängigkeiten zwischen den betrachteten Konstrukten auf.

Abb. 8: SEM zur Erkundung des Potenzials ortsbezogener Dienste für die Marktrecherche (Gansser/Krol 2017)

Die Messung von latenten Variablen wurde bereits im Abschnitt Dimensionsreduktion beschrieben. Der Aufbau und die Analyse eines SEM erfolgt im Wesentlichen in drei Schritten: Formulierung eines Modells, Modellschätzung und Auswertung des Modells:

Aufbau und Analyse eines SEM:

• Formulierung eines Modells: Strukturgleichungsmodelle werden auf der Grundlage theoretischer Überlegungen formuliert. Die Entwicklung des Modells für die Akzeptanz ortsbezogener Dienste (Abbildung 8) lässt sich z. B. aus vier grundlegenden Theorien zur Verhaltensforschung bei der Technologienutzung ableiten Theory of Reasoned Action (TRA), Theory of Planned Behavior (TPB), Technology Acceptance Model (TAM) und Theory of Acceptance and Use of Technology (UTAUT). Die Zusammenhänge zwischen den latenten Variablen stellen letztlich die zu untersuchenden Hypothesen dar.

Abb. 9: Reflektierende und formative Messmodelle

Für die Operationalisierung der latenten Konstrukte muss entschieden werden, ob eine reflexive oder formative Spezifikation der Messmodelle angemessen ist. Bei reflektiven Messmodellen wird angenommen, dass die Werte der beobachteten Indikatoren durch das latente Konstrukt verursacht werden. Eine Veränderung des latenten Konstrukts würde sich in einer Veränderung aller ihm zugeordneten Indikatoren niederschlagen. In formalen Messmodellen ist die Beziehung zwischen Indikatoren und latentem Konstrukt genau umgekehrt. Hier verursachen die beobachtbaren Indikatoren die Entwicklung des latenten Konstrukts.

• Modellschätzung: Die Schätzung der Parameter des Modells kann auf unterschiedliche Weise erfolgen. Grundsätzlich gibt es zwei verschiedene Ansätze.

  1. Ansatz: Für die meisten Forscher ist die SEM gleichbedeutend mit der Durchführung der kovarianzbasierten SEM (CB-SEM). Das Ziel der CB-SEM ist das Testen von Theorien, die Bestätigung von Theorien oder der Vergleich von alternativen Theorien. Die Parameterschätzung des Modells erfolgt gleichzeitig.
  2. Ansatz: SEM - Partielle Kleinstquadrate SEM (PLS-SEM). Das Ziel bei der varianzbasierten SEM (Partial Least Squares SEM oder PLS-SEM) ist die Vorhersage wichtiger Zielkonstrukte oder die Identifikation wichtiger Treiberkonstrukte. Die Faktorwerte werden zunächst sukzessive für die Messmodelle ermittelt und dann in einem zweiten Schritt als Messwerte für die latenten Variablen in einer Regressionsanalyse verwendet.

• Auswertung des Modells: Die Auswertung der Ergebnisse der Tests erfolgt mit verschiedenen Gütekriterien und inferenzstatistischen Tests. Sie wird in globale und lokale Gütekriterien unterschieden. Während globale Gütekriterien eine Beurteilung der Konsistenz des Gesamtmodells mit den erhobenen Daten erlauben, erlauben lokale Gütekriterien die Überprüfung der Messqualität einzelner Indikatoren und latenter Variablen. Dies hängt auch von der Art der Parameterschätzung ab. Wir verweisen an dieser Stelle auf die zahlreiche Spezialliteratur zur SEM.

3.1 Conjoint-Analyse

Die Conjoint-Analyse ist eine weit verbreitete und etablierte Methode zur Messung von Präferenzen. In der Praxis wird sie vor allem zur Preisabschätzung, Neuproduktplanung und zur Kundensegmentierung eingesetzt. Conjoint-Messungen sind im Vergleich zu anderen Verfahren eine realistischere Form der Präferenzmessung mit einer höheren Validität. Je nach Verfahren werden ein oder mehrere Produktkonzepte zur Bewertung vorgelegt. Die Produkte werden durch Merkmale definiert, die einen bestimmten Satz von Eigenschaften aufweisen. Der Proband ermittelt also für jede Ausprägung eines Merkmals gemeinsame Werte. Basierend auf den gemessenen Präferenzen kann eine Prognose generiert werden, welches Produkt bevorzugt und in Zukunft wahrscheinlich gekauft wird.

Die Conjoint-Analyse wurde im Marketing für eine Vielzahl von Zwecken eingesetzt, darunter die folgenden (Malhotra 2009):

• Bestimmung der relativen Wichtigkeit von Attributen im Entscheidungsprozess der Konsumenten.
• Schätzung des Marktanteils von Marken, die sich in der Ausprägung der Attribute unterscheiden.
• Bestimmung der Zusammensetzung der am meisten bevorzugten Marke.
• Segmentierung des Marktes basierend auf der Ähnlichkeit der Präferenzen für Attributniveaus.

Um diese Vorhersagen zu berechnen, werden Kaufentscheidungsmodelle angewendet. Für verschiedene hypothetische Produktalternativen werden Gesamtnutzenwerte geschätzt, die anschließend in Auswahlwahrscheinlichkeiten transformiert werden. Bei allen Modellen basiert die Auswahl auf den Prinzipien der Nutzenmaximierung, so dass Alternativen mit höherem Nutzen gegenüber solchen mit geringerem Nutzen bevorzugt werden. Die Verwendung solcher Entscheidungsmodelle für Prognosezwecke ist problematisch, wenn keine Informationen über die realen Kaufentscheidungsprozesse vorliegen und daher der Marktforscher eine individuelle Auswahl der Entscheidungsmodelle treffen muss. Dieser Nachteil besteht bei der Gruppe der traditionellen Conjoint-Analysen, bei denen die bewerteten Alternativen in ein Präferenzranking der Informationssubjekte gestellt oder mittels Ratingskalen bewertet werden. Dieser Nachteil entfällt bei der wahlbasierten Conjoint-Analyse, bei der die Personen aus verschiedenen Auswahlsets die attraktivste Alternative auswählen. Ein Choice-Set besteht aus zwei hypothetischen Alternativen und der Möglichkeit der Nicht-Auswahl. Es kann also davon ausgegangen werden, dass das natürliche Kaufverhalten der Person analysiert wird. Die wahlbasierte Conjoint-Analyse ist ein probabilistisches Verfahren zur Präferenzstrukturmessung. Die Teilnutzen der einzelnen Merkmale werden aus dem Gesamtnutzen geschätzt. Die Bewertungsobjekte werden anhand von Versuchsplänen konstruiert.

Vorgehensweise bei der Choice-basierten Conjoint-Analyse (Gansser und Füller 2015)

• Auswahl der Merkmalsausprägungen
• Definition des Versuchsplans
• Erstellung von orthogonal fraktionierten Choice-Sets
• Präsentation der Stimuli der Umfrageteilnehmer
• Schätzung der Nutzenfunktion

Abb. 10: Erste Auswahlmenge eines Seminarkonzepts (Gansser und Füller 2015)

Das Ergebnis der Conjoint-Analyse ist die Berechnung von Odds Ratios. Bei nominalen Merkmalen gibt das Odds Ratio (exp(coef)) einer Variablen die Chancen der Ausprägung eines Merkmals im Vergleich zur Basiskategorie an, also das Verhältnis eines Zufalls. Es ist dann möglich, die Merkmalsausprägung mit dem höchsten Chancenverhältnis als Beispiel für jedes Merkmal im Vergleich zu seiner Basiskategorie zu interpretieren. Das Chancenverhältnis von 5,7 für den Ort der Schulung und für die Ausprägung ausschließlich Präsenzseminar (T.1) signalisiert, dass die Chancen einer Buchung um das 5,7-fache zugunsten des Präsenzseminars (T.1) im Vergleich zur Basiskategorie Online-Seminare (T.1) steigen.

Abb. 11: Ergebnisse der Parameterschätzung der Nutzenfunktion (Gansser und Füller 2015)

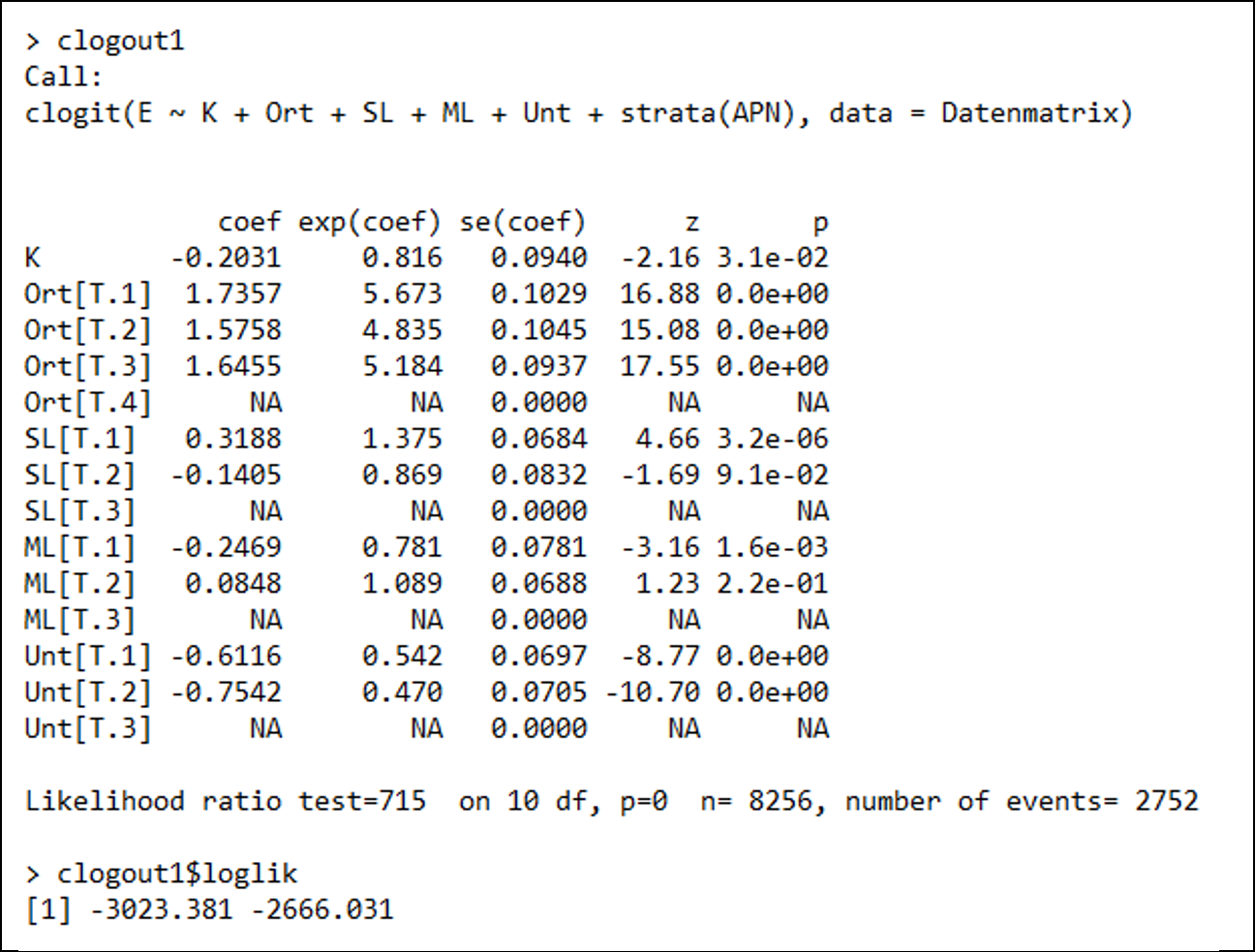
Schließlich kann mit der Conjoint-Analyse beantwortet werden, welches Angebot Personen bevorzugen und in Zukunft wahrscheinlich kaufen werden. Neben den Chancen eines Merkmals im Vergleich zu einer Grundform kann mit dieser Methode auch die Relevanz und damit die Wichtigkeit verschiedener Merkmale gemessen werden.

3.2 Marketing-Intelligenz

Ein Marketing-Intelligence-System umfasst eine Reihe von Verfahren, um alltägliche Informationen über Entwicklungen im Marketingumfeld zu erhalten. Der Zweck der Informationssammlung ist die genaue und sichere Entscheidungsfindung bei der Bestimmung des Marketingkonzepts (Ziele, Strategien und Aktivitäten). Sobald die Da-ta gesammelt sind (manuell oder automatisch), wird die Analyse in der Regel mit softwarebasierten Systemen durchgeführt. Der Ansatz der Intelligenz besteht darin, dass die Informationsquellen unterschiedlicher Natur sind und nach der Erfassung in eine einheitliche Umgebung gestellt werden. Ziel ist die integrierte Informationssammlung und -visualisierung von internen und externen Datenquellen. Dies ermöglicht die Betrachtung aktueller Kennzahlen (KPI) in Echtzeit oder so schnell wie die Daten erfasst werden können und die Analyse von Trends. Der Begriff “Business Intelligence” (BI) hat sich als Konzept für alle Methoden zur Analyse der Unternehmensleistung etabliert. So gibt es verschiedene Bereiche des Intelligence-Ansatzes, die darauf abzielen, die Teilleistung zu analysieren und zu optimieren. Neben der Marketing Intelligence hat sich auch der Bereich Sales Intelligence etabliert. In beiden Methoden besteht die Forderung nach einer integrierten Effizienzmessung über die Abteilungen hinweg. Der Trend geht dahin, dass klassische Controllingaufgaben von der zentralen Abteilung Controlling in die operativen Bereiche verlagert werden. Business Intelligence (BI) umfasst als geschlossenes System alle Analyse- und Optimierungsmöglichkeiten, die zur Erfassung, Analyse und Verbesserung von Geschäftsinformationen genutzt werden können.

Auswertungen im Rahmen von Intelligence-Ansätzen sollten folgende Anforderungen erfüllen:

• Auswertungen müssen in Echtzeit möglich sein.
• Zugänglichkeit innerhalb und außerhalb des Unternehmens mit Web-Anwendungen (auch mobile).
• Die Daten liegen in standardisierter und konsolidierter Form vor. Sie müssen nicht vom Anwender selbst gesammelt, konsolidiert und ausgewertet werden.
• Der Anwender kann die Analysen und Berichte an seine individuellen Anforderungen anpassen.
• Für die Analysen stehen Menüs für übersichtliche und aussagekräftige Diagramme zur Verfügung.
• Mehrdimensionale Analysen (OLAP) und Datenintegration aus allen Geschäftsbereichen führen zu neuen Erkenntnissen.

Um Daten aus dem Umfeld und dem strategischen Dreieck effizient zu erfassen, werden einige spezifische Datenquellen erschlossen, die sich besonders für das Marketing Intelligence eignen. Diese Daten können in der Regel vom Unternehmen selbst erhoben werden. Bei weniger sensiblen Daten gibt es auch die Möglichkeit, externe Agenturen zu beauftragen:

• Der Vertriebsmitarbeiter als freier Marktforscher: Der Außendienst ist die Person, die dem Kunden am nächsten ist. Sie können am einfachsten und ohne aufwändige Marktforschung beobachten, wie die Kunden die Produkte nutzen. Auf diese Weise können Ideen für neue Produkte generiert werden. Außerdem können Informationen über Wettbewerber und Händler erfasst werden.

• Mystery Shopping im Einzelhandelsgeschäft: Durch getarnte Mitarbeiter und deren Beobachtungen soll die Beratungsqualität und Kompetenz der Verkäufer ermittelt werden. Dies ist nicht unumstritten und sollte mit einem erweiterten Fokus auch auf die Qualität der Einrichtung versehen werden. Auch die Qualität des Kundenerlebnisses können Unternehmen mit dem Einsatz von Mystery Shoppern ermitteln.

• Wettbewerbsanalyse: Dies kann durch den Kauf von Produkten der Konkurrenz, die Überprüfung von Werbekampagnen, Presseberichten, das Lesen ihrer veröffentlichten Berichte usw. erfolgen. Die Wettbewerbsanalyse muss legal und ethisch einwandfrei sein.

• Kunden-Community: Die zu identifizierenden Kunden (Größe, Bedarf, Repräsentativität) können als Teilnehmer einer Community (online oder offline) oder eines Panels wertvolle Informationen zum Produkt, zur Produktnutzung und zu den Vertriebskanälen liefern. So können sie aktiv in die Verbesserungsprozesse des Unternehmens eingebunden werden. Online-Plattformen wie Chatrooms, Blogs, Diskussionsforen, Customer Review Boards können genutzt werden, um Kundenfeedback zu generieren. Dies ermöglicht es dem Unternehmen, die Erfahrungen und Eindrücke der Kunden zu verstehen.

• Offizielle Daten: Die Regierungen fast aller Länder veröffentlichen Berichte über die Bevölkerungsentwicklung, demografische Merkmale, landwirtschaftliche Produktion und andere Daten. Diese länderspezifischen Basisdaten können bei der Planung von Geschäftskonzepten hilfreich sein.

3.3 Risikoanalyse mit Monte-Carlo-Simulation

Bei der Marketingplanung wird versucht, die Zukunft in Zahlen zu fassen. Ausgehend von Annahmen werden Zukunftswerte ermittelt und Zielgrößen berechnet. Für die Berechnung der Zielgröße wird ein Modell mit Ursache-Wirkungs-Beziehungen gebildet. Da die Zielgrößen unbestimmt sind, werden in einer Risikoanalyse verschiedene Risikoszenarien für verschiedene Szenarien ermittelt.

Bei der Monte-Carlo-Methode werden Zufallszahlen simuliert. Im Mittelpunkt der Simulation steht ein Zufallszahlengenerator, der Zufallszahlen erzeugt, deren Verteilung der jeweils betrachteten Wahrscheinlichkeitsverteilung entspricht. In jedem Simulationslauf wird für jede Einflussgröße ein Wert durch Zufallsauswahl ermittelt, wobei beliebig viele Simulationen durchgeführt werden können. Der Ergebniswert wird mit den Realisierungen aller Einflussgrößen berechnet. Mit anderen Worten: Die Monte-Carlo-Simulation erzeugt Verteilungen möglicher Ergebnisse. Nach einer hinreichend großen Anzahl von Simulationen können dann die Wahrscheinlichkeitsverteilung und die relevanten Kenngrößen wie Mittelwert, Varianz und Konfidenzintervall berechnet werden. Eine anwendungsbezogene Einführung in die Monte-Carlos-Simulation geben Robert und Casella 2009.